Le 17 equazioni che hanno cambiato la nostra vita
La matematica è un’arte e non serve capirla per apprezzarla! Lo sostiene Ian Stewart, matematico autore del libro «In Pursuit of the Unknown: 17 Equations that Changed the World». Un viaggio tra le 17 equazioni che hanno cambiato la nostra vita da Pitagora ad Albert Einstein.
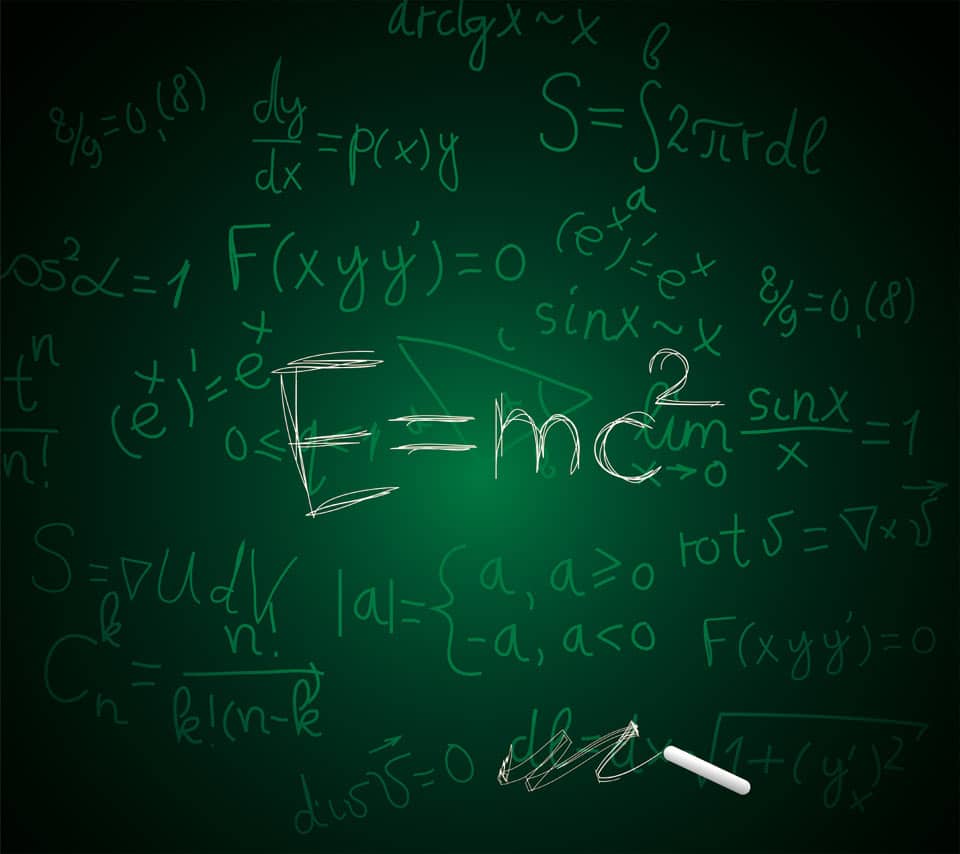
E=mc2, credits: http://m-static.flikie.com/
Quanto è importante la matematica e quanto incide nel progresso tecnologico della società? Questa disciplina gioca senz’altro un ruolo di attacco nella formazione della scienza, sebbene molto spesso la sua complessità renda poco comprensibili dimostrazioni e contenuti. Ma non per questo dobbiamo odiarla! La matematica è un’arte e se avete difficoltà nel capirla non vi preoccupate: «Si possono apprezzare la bellezza e l’importanza delle equazioni anche senza sapere come si risolvono», sostiene il matematico Ian Stewart in un’intervista rilasciata a Business Insider Uk.
Autore del libro «In Pursuit of the Unknown: 17 Equations that Changed the World»: un testo affascinante in cui Steward racconta le equazioni, come sono state scoperte e i loro usi nel mondo antico e moderno. Scopriamo quali sono! Dal noto Teorema di Pitagora al logaritmo, dal calcolo differenziale alla grandiosa Legge di gravitazione universale di Newton senza trascurare Gauss, D’Alembert, Fourier, Navier-Stokes, Maxwell ed ovviamente l’amato Albert Einstein. Un libro affascinante che rischia di far appassionare anche chi, la matematica, non l’ha mai digerita! Purtroppo il libro, pubblicato nel 2012, non è ancora approdato in Italia ma se l’inglese non è vostro nemico, non avrete difficoltà a lasciarvi trasportare dai numeri, dalla logica e da un lessico piacevole e travolgente anche per i non addetti ai lavori. Ma adesso andiamo alla scoperta di quelle che sono le 17 equazioni che hanno cambiato il mondo!
- Il Teorema di PitagoraIn un triangolo rettangolo, il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati sui cateti. Tutti si ricordano il Teorema di Pitagora, anche se non è certo che sia stato proprio lui a provarne la validità per la prima volta. C’è chi ritiene che siano stati addirittura i Babilonesi a scoprirlo e sicuramente si sa che una prova chiara è stata fornita d Euclide.
Questa equazione è alla base della geometria, la collega all’algebra e è uno dei fondamenti della trigonometria. Senza il teorema di Pitagora sarebbe impossibile disegnare mappe accurate e fare la maggior parte dei calcoli per la navigazione. Per non parlare del Gps che non esisterebbe. - Formula di Eulero per i poliedri
Sviluppata nel 18esimo secolo dal matematico Leonhard Euler, la formula è usata per capire la funzione del Dna, ma anche i social media e internet.
3. Il logaritmo e le sue identità
I logaritmi furono scoperti da Nepero, un proprietario terriero scozzese con la passione per la matematica, nel 1614. Furono rivoluzionari perché grazie anche alle tavole logaritmiche permisero per secoli di moltiplicare grandi numeri in modo facile e veloce.
Oggi, grazie all’avvento dei computer, hanno perso parte del loro interesse ma restano fondamentali per l’accuratezza dei calcoli ingegneristici e astronomici. Sono utili in molti settori scientifici, dal calcolo della crescita biologica a quello degli interessi composti.
4. Il calcolo differenziale
Il calcolo differenziale fu descritto alla fine del diciassettesimo secolo da Isaac Newton e da Gottfried Leibniz. E’ ancora in corso la disputa per decidere chi dei due sia arrivato per primo alla definizione del calcolo differenziale anche se sembra che i due studiosi ci siano arrivati per vie diverse e indipendenti.
La legge di gravitazione universale di Isaac Newton afferma che nell’Universo ogni punto materiale attrae ogni altro punto materiale con una forza che è direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della loro distanza.
La legge di Newton, superata dalla teoria della relatività di Einstein, è tuttavia ancora essenziale per spiegare come si comportano gli oggetti in movimento nello spazio, da una palla che cade fino ai satelliti.Per numero complesso si intende un numero formato da una parte immaginaria e da una parte reale. Può essere perciò rappresentato dalla somma di un numero reale e di un numero immaginario (cioè un multiplo dell’unità immaginaria, indicata con la lettera i). I numeri complessi sono usati in tutti i campi della matematica, in molti campi della fisica (e notoriamente in meccanica quantistica), nonché in ingegneria, specialmente in elettronica/telecomunicazioni o elettrotecnica, per la loro utilità nel rappresentare onde elettromagnetiche e correnti elettriche ad andamento temporale sinusoidale.
Ogni equazione ha una soluzione con i numeri immaginari, cosa che non avviene necessariamente con i numeri reali. La loro importanza pratica secondo Ian Steward, autore del libro “In Pursuit of the Unknown: 17 Equations that Changed the World”, è molto grande edè essenziale per capire i sistemi elettrici e una varietà di algoritmi di elaborazione dei dati: per esempio, le macchine fotografiche digitali non sarebbero state inventate.7. La distribuzione normale o di Gauss
Nella teoria della probabilità la distribuzione normale, o di Gauss (o gaussiana) dal nome del matematico tedesco Carl Friederich Gauss, è una distribuzione di probabilità continua che è spesso usata come prima approssimazione per descrivere variabili casuali a valori reali che tendono a concentrarsi attorno a un singolo valor medio. Il grafico della funzione di densità di probabilità associata è simmetrico e ha una forma a campana, nota come campana di Gauss (o anche come curva degli errori, curva a campana, ogiva).
8. Equazione delle onde o di D’Alembert
Questa equazione differenziale descrive il comportamento delle onde, come il comportamento di una corda di violino che vibra.
Serve per vedere come funziona il suono, come succedono i terremoti, e il movimento degli Oceani.
9. La Trasformata di Fourier
Elaborata nel 1822 dal matematico francese Jean Baptiste Joseph Fourier, permette di scrivere una funzione dipendente dal tempo nel dominio delle frequenze. Ha tantissimi usi nella scienza applicata: dalla compressione delle informazioni delle imagini Jpeg alla descrizione della struttura delle molecole.
10. Equazioni di Navier-Stokes
Le equazioni di Navier-Stokes sono un sistema di equazioni differenziali alle derivate parziali che descrivono il comportamento di un fluido dal punto di vista macroscopico. L’ipotesi di base è che il fluido possa essere modellato come un continuo deformabile.
11. Le equazioni di Maxwell
Descrivono la relazione tra campi elettrici e campi magnetici. Sono per l’elettromagnetismo quello che le leggi di Newton sul movimento sono per la meccanica. Jeames Clerk Maxwell ha tradotto in equazioni il lavoro di Michael Faraday sul rapporto elettricità/magnetismo.
La formulazione più diffusa del secondo principio della termodinamica è quella di Clausius: «È impossibile realizzare una trasformazione il cui unico risultato sia quello di trasferire calore da un corpo più freddo a uno più caldo senza l’apporto di lavoro esterno».
13. La teoria della relatività di Einstein
É la più famosa equazione della storia e mette in relazione energia e materia. Formulata nel 1915 (relatività generale) da Albert Einstein ha rivoluzionato il mondo della fisica.
14. L’equazione di Schroedinger
In meccanica quantistica è un’equazione fondamentale che determina l’evoluzione temporale dello stato di un sistema, ad esempio di una particella, di un atomo o di una molecola. Formulata dal fisico austriaco Erwin Schrödinger nel 1927 si basa sul principio che le particelle che costituiscono la materia, come l’elettrone, hanno un comportamento ondulatorio.
15. L’entropia dell’informazione (teoria di Shannon)
Misura, così come il secondo principio della termodinamica, il contenuto informativo medio di un messaggio, sia un libro, una foto Jpeg o qualsiasi altro elemento che può essere rappresentato con un simbolo. E’ una misura di disordine
Grazie alla teoria di Shannon si è potuto cominciare a studiare con un modello matematico l’informazione e i risultati sono centrali per comunicare nei network.
16. La mappa logistica
La mappa logistica è spesso citata come un esempio di come un comportamento complesso, caotico può sorgere da una semplice equazione dinamica non lineare. La mappa fu resa popolare nel 1976 dal biologo Robert May. E’ servita per lo sviluppo della teoria del caos che ha completamente cambiato la nostra comprensione del modo in cui funziona un sistema naturale.
17. Il modello di Black-Scholes
Il modello di Black-Scholes-Merton (gli ultimi due hanno vinto il Nobel perl ‘economia nel 1977 per questa scoperta) rappresenta l’andamento nel tempo del prezzo di strumenti finanziari, in particolare delle opzioni.
