Fibonacci? No, mi chiamo Leonardo!
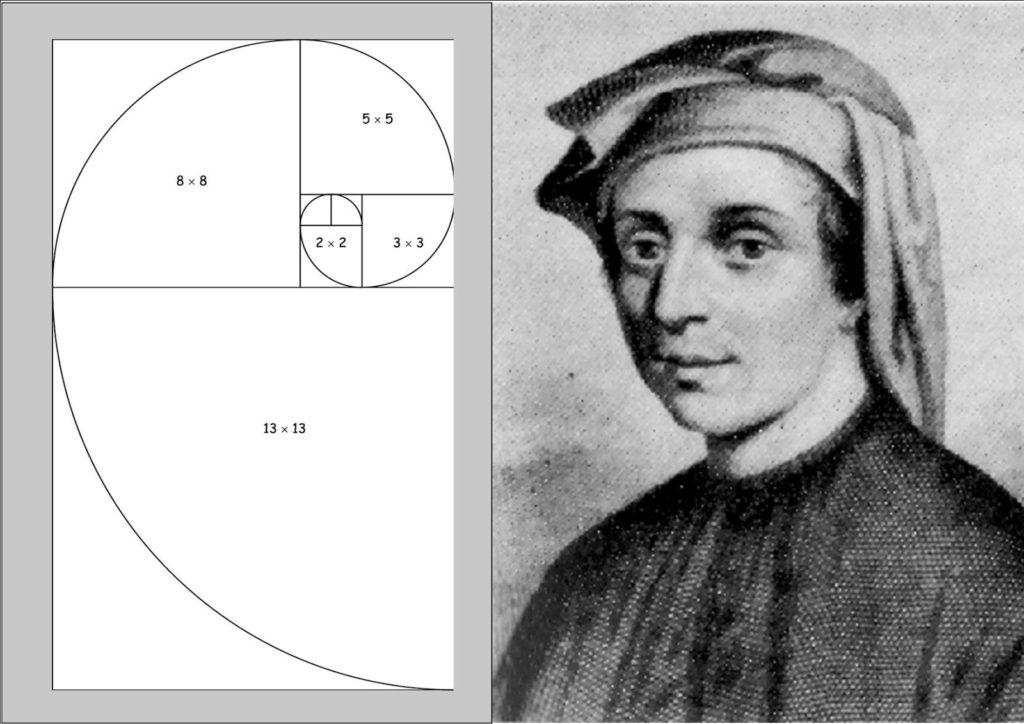
Se qualcuno lo avesse fermato per strada, chiamandolo Fibonacci, Leonardo da Pisa (questo il suo vero nome) lo avrebbe guardato male. Apparteneva ad una famiglia di Pisa che si era data un nome da sola, la famiglia Bonacci, e così qualche secolo dopo uno storico (non sappiamo di preciso chi) lo ha definito come fi’ Bonacci, “figlio di Bonacci”. Se qualcuno gli avesse parlato della successione di Fibonacci, Leonardo da Pisa non avrebbe capito a cosa si riferisse.
Fibonacci e le terne Pitagoriche

E’ stato il matematico francese Edouard Lucas a chiamare così per la prima volta nel maggio del 1876 la successione che nasce dal problema di riproduzione di conigli contenuto nel “Liber abaci”. Se qualcuno avesse cercato un collegamento tra la successione di Fibonacci e il teorema di Pitagora, probabilmente sarebbe stato preso per pazzo.
Invece, sorprendentemente, nel 1948 il matematico Charles Raine ha scoperto che è possibile utilizzare i numeri di Fibonacci per generare terne pitagoriche (cioè terne di interi positivi come 3,4,5 che, se interpretati come misure, corrispondono ai lati di un triangolo rettangolo). Vediamo come: prendiamo quattro numeri qualsiasi consecutivi nella successione di Fibonacci, come 3, 5, 8, 13. Il prodotto degli estremi (3 x 13, cioè 39), il doppio del prodotto dei medi (2 x 5 x 8, cioè 80) e la somma dei quadrati dei medi (5^2+8^2, cioè 89) formano una terna pitagorica: infatti, 39^2+80^2=1521+6400=7921=89^2. Ma non finisce qui: il terzo numero della terna, 89 (corrispondente all’ipotenusa del triangolo rettangolo), è esso stesso un numero di Fibonacci!
