Ian Stewart e il paranormale nella matematica
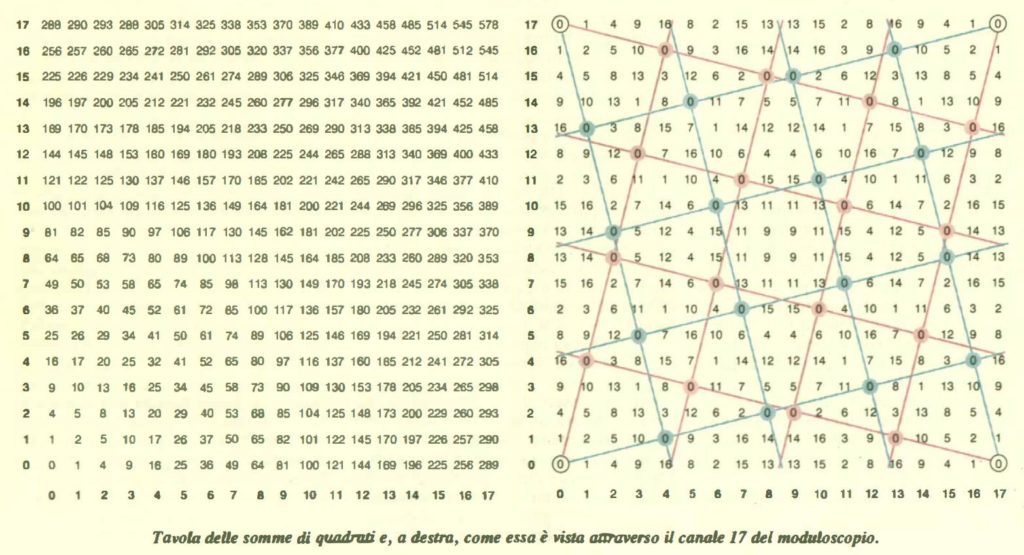
Tavola delle somme di quadrati e, a destra, come essa è vista attraverso il canale 17 del moduloscopio.
“Oddio, deve essere un altro fantasma” pensò Stooge. “I guai vengono sempre tre alla volta”. Si rivolse verso il soffitto e urlò: “Forza, materializzati, non possiamo perderci tutta la notte!”. “Io sono il Fant… etciù! il Fantasma delle dimostrazioni presenti. Si gela qui dentro! Ma non accendi mai il fuoco?”. Il fantasma si soffiò rumorosamente il naso in un lembo di ectoplasma. “Sei venuto qui per farmi vedere come si dimostra che ogni numero primo della forma 4k+1 è la somma di due quadrati?”. “Proprio così, ragazzo mio! Ci toccano sempre dei lavoracci, a noi fantasmi! Ma non perdiamo tempo, Ebeneezy Stooge. Metti il tuo quadrante su canale 17 e tutto sarà chiaro!”. Con ampio gesto, il Fantasma delle dimostrazioni presenti tirò fuori un foglio di plastica suddiviso in quadrati e lo mise sul tavolo. “Ti farò vedere la dimostrazione per il numero primo 17, ma lo stesso metodo funziona per tutti. L’idea, amico mio, è smettere di pensare ai numeri primi e iniziare a pensare alle somme di quadrati. Su questo foglio speciale ci sono tutte le possibili somme di due quadrati, con x^2+y^2 scritto nella colonna x e nella riga y. Guardalo attraverso il moduloscopio. Che cosa vedi?”. “Un sacco di numeri compresi tra 0 e 16, dappertutto”. “Hmm, già, che stupido sono. Prendi questo pennarello e segna dei puntini ovunque vedi uno zero”. Stooge disegnò una strana configurazione periodica di punti (si veda l’illustrazione in figura), stette un pò a osservarla, poi scosse la testa con aria perplessa. “C’è uno schema nascosto” disse il fantasma. “Fammi colorare in rosso alcuni dei punti e gli altri in azzurro… Vedi qualcosa?”..”Caspita! Sono due griglie regolari,una sovrapposta all’altra!”. “Esatto! Il nome giusto per una griglia di questo genere è reticolo. I punti che hai disegnato sono tutti i punti (x,y) della colonna x e della riga y tali per cui x^2+y^2 è un multiplo di 17. Ora, guarda il reticolo rosso e dimmi qual è il punto più vicino all’origine (colonna 0, riga 0)”. “Facile. E’ nella colonna 1, riga 4”. “E quale multiplo di 17 è la somma di quadrati corrispondenti?”. “1^2+4^2=17 stesso! Ora capisco! Mi stai dicendo che il punto del reticolo rosso più vicino all’origine risolve il problema di rappresentare 17 come somma di due quadrati!”. “Sì. Anche il reticolo azzurro funziona, ma dà la soluzione rovesciata, 4^2+1^2. Fai un’altra prova:questa volta metti il tuo quadrante su canale 41. Hai lo stesso tipo di risultato?”. “Sì! Guarda, abbiamo ancora due reticoli sovrapposti! Il punto più vicino all’origine nel reticolo rosso si trova in colonna 4, riga 5; 4^2+5^2 è uguale a 41!”. “Grandioso! Puoi divertirti a provare altri canali sul moduloscopio. Scegli un tuo numero primo p e segna tutte le posizioni (x,y) con x^2+y^2 multiplo di p. Otterrai sempre una configurazione formata da due reticoli, anche se probabilmente non lo avresti notato se non ti fosse stato detto. Ma io sono il Fantasma delle dimostrazioni presenti, non degli esempi! Devo spiegare perché ci sono due reticoli, e perché il punto del reticolo più vicino all’origine risolve sempre il problema!”.
Ian Stewart
