Il problema delle coppie perfette: dal matrimonio all’università dei sogni

Il tema dell’amore, o più in generale delle relazioni interpersonali, è diventato oggetto di studio in varie branche della Matematica nel corso del XX secolo. Sergio Rinaldi, docente di matematica del Politecnico di Milano, è stato il primo a studiare seriamente le relazioni amorose da un punto di vista matematico, partendo dall’analisi di una delle opere poetiche più romantiche che siano mai state scritte: il Canzoniere di Petrarca. La sua opera è raccolta nel testo “Modeling Love Dynamics”, pubblicato nel 2016 da World Scientific.

Cambiando punto di vista, Gale e Shapley nel 1962, hanno introdotto il cosiddetto Problema del matching che ricade nell’ambito della Teoria dei Giochi. In questo articolo andremo ad analizzare quest’ultimo problema, ma prima consideriamo alcuni esempi:

• In un villaggio, isolato dal resto del mondo, si trova un gruppo di donne e di uomini che, avendo raggiunto la maggiore età, si devono sposare entro la fine dell’anno. Il capovillaggio è incaricato di celebrare i matrimoni e deve decidere quali siano le coppie da formare in modo che tutti i giovani siano felicemente sposati, senza divorzi e tradimenti. Come può fare?
• Un gruppo di studenti, terminati gli anni delle scuole superiori, si trova di fronte ad una delle scelte più importanti della propria vita: la scelta dell’università. Stilano pertanto una lista in base alle loro preferenze. D’altro canto, però, le università non possono accogliere tutte le domande e quindi dovranno redigere un ranking sugli studenti. Come è possibile far sì che nessuno studente sia scontento e pertanto invogliato a cambiare facoltà?
• Il primario di un ospedale si trova di fronte il nuovo gruppo di specializzandi. Ognuno ha ambizioni e interessi diversi e quindi è necessario che a ciascuno di essi venga assegnata una specializzazione in linea con le aspettative. Come può fare il primario per evitare scontenti all’interno del suo staff?

Questi problemi, sebbene apparentemente molto diversi, possono essere messi a fattor comune sotto un’unica teoria e trattazione, che andremo a scoprire passo per passo. Prendiamo in esame il caso di matching tra uomini e donne, ma tutti i ragionamenti possono essere ripetuti sostituendo i ruoli con gli altri attori presentati.

Il problema

La formulazione del problema prevede due insiemi \(\mathcal{M}\) e \(\mathcal{W}\) con la stessa cardinalità (i.e. con lo stesso numero di elementi). Ogni elemento di \(\mathcal{W}(\mathcal{M})\) ha un ranking, indicato con \(>_m\) e \(>_W\) rispettivamente, sugli tutti gli elementi di \(\mathcal{M}(\mathcal{W})\).  L’obiettivo è formare coppie stabili. Per esempio se

$$ \begin{aligned}
\mathcal{W}&=\{\text{Anna,Giulia,Maria}\}\\
\mathcal{M}&=\{\text{Marco,Luca,Giovanni}\}
\end{aligned}$$

un possibile matching è dato da

$$ \Lambda=[(\text{Anna,Marco}),(\text{Giulia,Luca}),(\text{Maria,Giovanni})]$$

Non abbiamo ancora specificato però cosa si intende con coppie stabili. Definiamo un matching stabile se nessuna coppia obietta. Una coppia obietta qualora sia l’uomo che la donna si preferiscano a vicenda rispetto alla persona con cui sono stati accoppiati. Ad esempio, se nel matching precedente

$$ \text{Marco}>_{\text{Giulia}}\text{Luca}\quad\text{Giulia}>_\text{Marco}\text{Anna}$$

allora non sarà stabile.

Un algoritmo per la soluzione

Fortunatamente, ogni problema di matching ammette una soluzione stabile. Vediamo allora come fare a trovare le coppie, assumendo che tutti preferiscano essere accoppiati piuttosto che rimanere soli. Per semplicità di notazione, indichiamo gli uomini con lettere minuscole e le donne con lettere maiuscole. Le preferenze sono le seguenti

$$ \begin{aligned}
& A>_aB>_aC\quad &B>_bA>_bC \quad&A>_cB>_cC\\
& a>_Ab>_Ac\quad &b>_Ba>_Bc\quad&a>_C b >_C c
\end{aligned} $$

Per trovare un matching stabile ricorriamo all’algoritmo di visita:

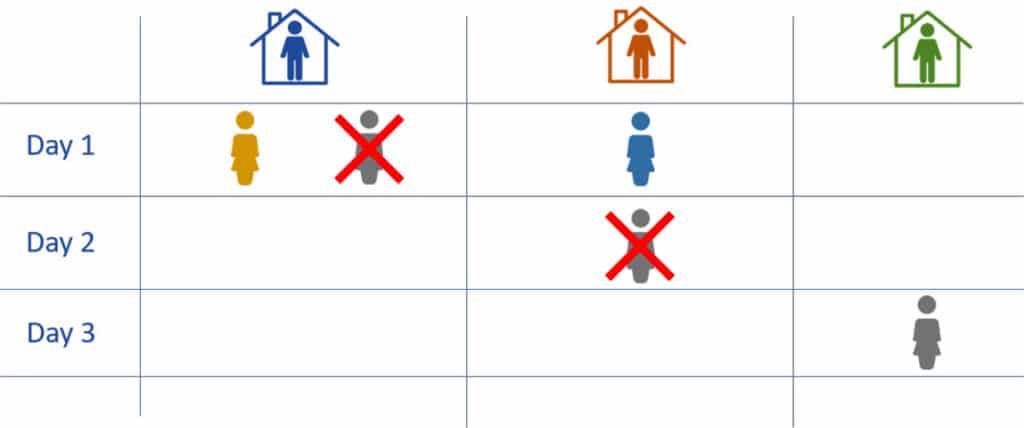
1. Il primo giorno ogni donna si reca dalla sua prima scelta. Se ogni uomo si trova con una sola donna l’algoritmo termina. Altrimenti, l’uomo (o gli uomini) che si trova con più di una scelta sceglie in base al suo ranking.
2. Il secondo giorno le donne rifiutate si recano dalla loro seconda scelta. Analogamente al giorno 1, gli uomini possono accettare o scegliere in base al loro ranking.
3. L’algoritmo termina quando tutte le donne hanno trovato una compagna.

Con i profili riportati sopra otteniamo il seguente matching stabile:

$$ \{(a,A),(c,B),(b,C)\}$$

La soluzione è unica?

In generale la risposta è negativa. Infatti, non vi è ragione per affermare che, invertendo i ruoli di uomini e donne nell’algoritmo, si giunga alla stessa soluzione. Per il problema precedente, invertendo i ruoli, si giunge ad un secondo matching:

$$ \{(a,A),(b,B),(c,C)\}$$

Articolo a cura di Mirko Baroni.