Bernoulli: qual è la curva per passare da A a B nel tempo più breve?

Una delle storie più affascinanti di tutta la matematica ebbe inizio nel giugno del 1696 quando, sulle pagine degli Acta eruditorum, Johann Bernoulli propose il seguente problema. Egli immaginava due punti A e B, a differenti altezze rispetto al suolo ma non situati direttamente uno sotto l’altro. Ci sono infinite curve che congiungono tali punti e il tempo impiegato da una pallina che scivoli lungo una di queste curve a completare il percorso (supponendo che non ci sia attrito e che la pallina, inizialmente ferma, scivoli giù sotto l’azione del suo stesso peso, senza essere in alcun modo spinta) dipende, ovviamente, dalla forma della curva.

Uno sguardo al problema diBernoulli

Bernoulli sfidava i matematici del suo tempo a trovare la particolare curva che consentisse alla pallina di passare da A a B nel tempo più breve. Chiamò tale curva “brachistocrona“, dalle parole greche che significano appunto “più breve” e “tempo”. La prima e più ovvia tentazione era quella di pensare al segmento che unisce i due punti ma Johann metteva subito in guardia da un approccio così semplicistico. “Per prevenire giudizi affrettati, dirò che la linea retta AB è sì la più breve tra i punti A e B, ma non è quella che si percorre nel minor tempo. La curva che cerchiamo, il cui nome rivelerò se nessun altro la avrà scoperta entro la fine di quest’anno, è una curva ben nota agli studiosi di geometria”.

La sfida fu ben accolta dal marchese de l’Hopital, per esempio, che subito rispose: “Questo problema mi sembra fra i più curiosi e graziosi mai proposti, e mi piacerebbe assai applicarmici, ma per questo sarebbe necessario che voi me lo mandaste ridotto alla matematica pura, perché la fisica mi mette a disagio…”.

Johann aveva fissato al primo gennaio 1697 il termine ultimo per presentare una soluzione. Ma in quella data aveva ricevuto un’unica risposta, quella del “celebre Leibnitz”, il quale però “mi ha cortesemente domandato di prolungare la scadenza fino alla prossima Pasqua, affinché nel frattempo il problema possa essere reso pubblico […] e perché nessuno abbia ragione di lamentarsi della ristrettezza del tempo concesso.

Non solo ho convenuto con una richiesta così ragionevole, ma ho deciso di annunciare io la proroga per vedere chi saprà affrontare questo problema così difficile ed elevato e, dopo tanto tempo, finalmente risolverlo”. Poi, per essere sicuro che non ci fossero equivoci sul problema, lo ripeté: “Tra le infinite curve che congiungono i due punti dati, […] trovare quella che, quando venga sostituita da un tubo sottile o da una scanalatura in cui sia posta e lasciata libera una piccola sfera, allora quest’ultima possa andare da un punto all’altro nel tempo più breve”. In Europa, all’approssimarsi della Pasqua, giunsero a Bernoulli alcune soluzioni.

Un nuovo punto di vista sulla cicloide

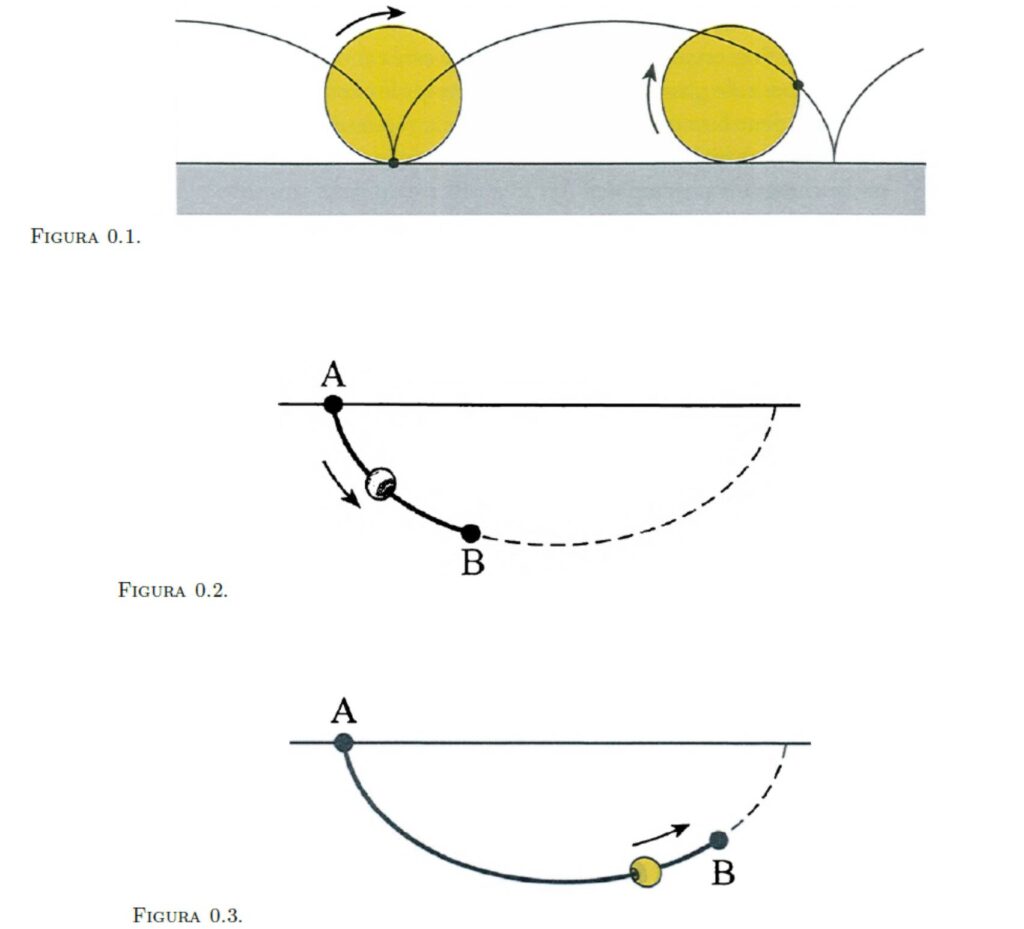
La curva che tutti stavano cercando, una curva “ben nota agli studiosi di geometria”, altro non era che la cicloide, cioè la curva tracciata da un punto fisso sul bordo di un cerchio che rotola senza strisciare su una superficie piana (si veda la figura 1). L’idea era di costruire una cicloide delle dimensioni opportune, capovolgerla e farla passare attraverso i punti A e B assegnati (si veda la figura 2). Il fatto più curioso di tutti era che, a seconda della posizione relativa di A e B, la curva che corrispondeva alla discesa più celere poteva anche passare sotto B prima di risalire! (si veda la figura 3).

La cicloide era stata già studiata dettagliatamente da Pascal e da Huygens, ma stranamente nessuno dei due si era accorto che essa possedesse anche la proprietà di essere la curva di discesa più rapida. Johann scrisse con la sua caratteristica enfasi: “Sarete pietrificati dallo stupore quando vi dirò che è proprio questa cicloide [..] di Huygens la brachistocrona che cercavamo”. A Pasqua, quando il nuovo termine era scaduto, in tutto Johann aveva ricevuto 5 soluzioni. C’erano la sua e quella di Leibniz; quella del fratello Jakob (con grande costernazione di Johann) e quella mandata dal marchese de L’Hopital.

Infine, c’era un plico giunto dall’Inghilterra. Johann lo aprì e vi trovò una soluzione esatta ma non firmata. In realtà non c’era alcun bisogno della firma per riconoscere l’impronta del genio di Newton. Johann, un po’ esterrefatto e un po’ abbattuto, posò il manoscritto anonimo e disse: “Riconosco il leone dal suo artiglio”.