Far crollare un ponte camminando: il fenomeno della risonanza spiegato

Era il 12 aprile 1831, quando un gruppo di 74 soldati britannici tornando da un’esercitazione attraversò in marcia il Broughton Suspension Bridge in quella che è l’odierna città di Salford in Inghilterra. Al passaggio dei militi il ponte cominciò a vibrare sempre più violentemente fino a giungere al collasso. Fortunatamente non ci fu alcuna vittima, ma venti uomini rimasero feriti. Di primo acchito si potrebbe pensare ad un qualche errore di progettazione o alla mancanza di una adeguata manutenzione, ma in realtà la causa del crollo del ponte fu semplicemente il passo di marcia dei soldati. Proprio così, il semplice camminare di un gruppo di persone può portare al collasso di una struttura imponente come un ponte. Incredibile vero? Eppure, questo fenomeno che sta alla base del collasso del Broughton Bridge è piuttosto noto in meccanica e prende il nome di risonanza.

Tutti gli oggetti possono di regola entrare in risonanza vibrando e quando ciò accade – se questa non è cercata intenzionalmente – il loro destino è quello di rompersi. Alcuni esempi in questo senso sono le ali di un aeroplano che oscillano a causa dell’interazione con l’aria circostante, oppure un bicchiere da vino che viene eccitato dalla voce di una cantante lirica, o ancora, un ponte sollecitato dal vento come accadde nel 1940 per il noto crollo del Tacoma Narrows Bridge. In alcuni casi, però, le vibrazioni sono appositamente indotte in un corpo: per esempio le vibrazioni dei dispositivi elettronici (telefoni, joystick, eccetera…) oppure gli altoparlanti che producono suono forzando l’oscillazione di una membrana.

Il Tacoma Narrows Bridge, situato nello stato di Washington, cedette nel 1940 in seguito a forti raffiche di vento che ne forzarono l’oscillazione. In realtà, il ponte probabilmente non entrò davvero in risonanza, ma crollò a causa di un progressivo danneggiamento dovuto al “flattering”. (Fonte: Library of Congress, Washington, DC).

La risonanza

Tutti gli oggetti di cui facciamo esperienza nel quotidiano possono vibrare, d’altronde è facile verificarlo, basta prendere un oggetto qualsiasi e colpirlo per sentirlo emettere un suono. Anche il suono, infatti, viene originato a partire da una vibrazione. Ma che cosa sono le vibrazioni? Potete pensare alla vibrazione di un oggetto come una continua oscillazione – uno spostamento – rispetto ad un suo punto di equilibrio. Prendete ad esempio un bambino su un’altalena che dondola avanti e indietro, oppure una corda di chitarra che viene pizzicata dal plettro. Entrambi questi casi sono esempi di quello che in meccanica si definisce come “vibrazione”, l’unica differenza è che la prima è caratterizzata da una bassa frequenza, mentre la seconda si verifica a frequenze ben più alte.

La frequenza è un parametro molto importante quando si parla di vibrazioni, questa grandezza esprime la quantità di oscillazioni che avvengono al secondo e si misura in Hertz (Hz). La cosa interessante è che ogni oggetto possiede una sua frequenza propria detta frequenza naturale, la quale dipende sostanzialmente dalla massa dell’oggetto e dalle sue caratteristiche meccaniche – più precisamente dalla rigidezza. Tutti gli oggetti quando vibrano “liberamente” – ad esempio pensate a quando si colpisce un bicchiere con una forchetta e lo si lascia vibrare – lo fanno alla loro frequenza naturale. Il problema sorge quando una sollecitazione esterna forza l’oggetto a vibrare con una frequenza vicina a quella naturale. In questo caso, infatti, l’intensità delle vibrazioni si fanno molto forti anche se la sollecitazione che le provoca è piccola. Quando ciò avviene si dice che il sistema è entrato in risonanza.

Un esempio pratico: l’oscillatore armonico

Il sistema meccanico più semplice da studiare per comprendere il fenomeno della risonanza è sicuramente l’oscillatore armonico. Questo modello è costituito da una massa vincolata all’estremità di una molla che oscilla in una sola direzione. In questo specifico esempio considereremo una massa di 1 kg appesa ad una molla (avente costante elastica 100 N/m).

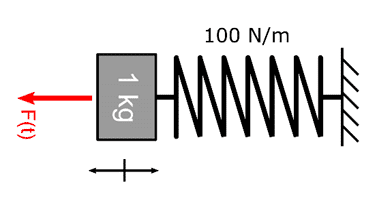
L’oscillatore armonico è un semplice modello che consiste in una massa vincolata ad una molla. In questo caso l’oscillazione avviene in verticale. Piccola nota tecnica: la presenza della gravità può essere trascurata in quanto non cambia il comportamento della vibrazione, ma solamente la posizione di equilibrio della molla.

Da queste caratteristiche – come spiegato nel paragrafo precedente – possiamo ricavare la frequenza naturale del sistema che in questo caso vale 1.6 Hz. Immaginiamo poi di spingere avanti e indietro la massa inizialmente ferma con una forza di 10 N per vedere come questa risponde alla nostra sollecitazione. Tralasciando tutta la trattazione matematica che si addice più ad un contesto accademico che di divulgazione scientifica, possiamo passare direttamente alla soluzione del problema.

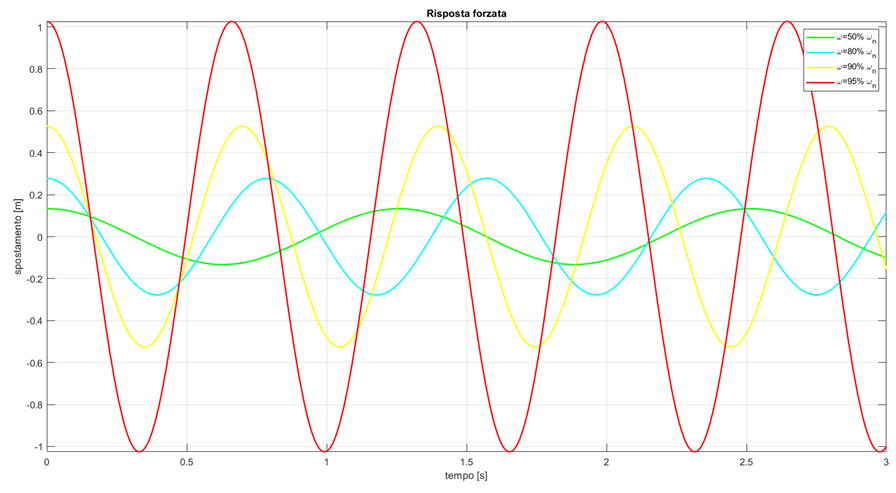
Come ci si poteva aspettare da quello che abbiamo detto finora, vediamo che la risposta dell’oscillatore armonico varia in base alla frequenza con cui lo costringiamo a vibrare. In particolare, quando la frequenza si avvicina a quella naturale del sistema vediamo che l’intensità della vibrazione – rappresentata dallo spostamento della massa – si fa sempre più alta nonostante la forza rimanga sempre la stessa. Questo principio viene ampiamente sfruttato anche nell’industria per muovere i prodotti lungo la catena di produzione facendo vibrare dei supporti a mezzo di piccole sollecitazioni. L’obbiettivo in questa circostanza è quello di risparmiare energia per il trasporto dei prodotti.

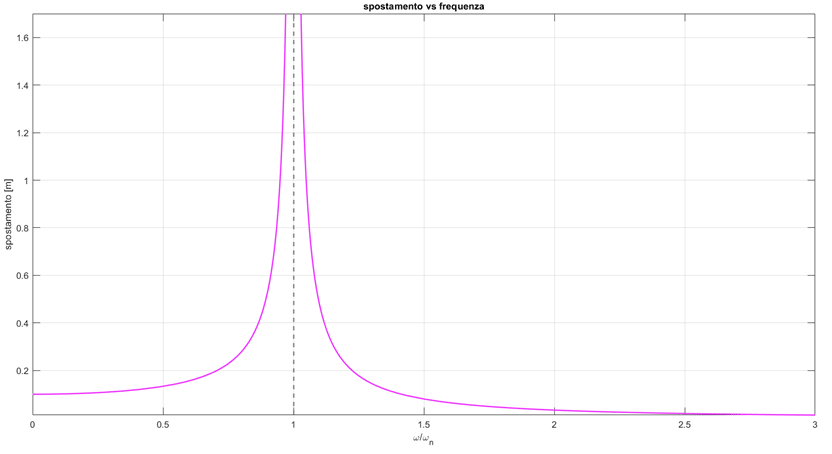
La risposta forzata dell’oscillatore armonico diventa sempre più intensa – ovvero lo spostamento della massa aumenta – man mano che la frequenza forzante si avvicina a quella naturale. Ciò avviene nonostante l’intensità della sollecitazione sia sempre la stessa (10 N).

Un altro modo comune per visualizzare l’effetto che la risonanza ha sulla risposta dell’oscillatore armonico è quello di guardare come cambia l’intensità dello spostamento della massa al variare della frequenza forzante. Quando la frequenza forzante eguaglia esattamente la frequenza naturale del sistema, teoricamente avremmo uno spostamento infinito della massa. Ovviamente in realtà questo non è possibile, perché la molla ad un certo punto si romperebbe. Una volta raggiunta la risonanza, ammesso che l’oggetto vi sopravviva, all’aumentare della frequenza forzante l’intensità delle vibrazioni diminuisce fino a rendere nullo l’effetto della sollecitazione.

Quando la frequenza forzante eguaglia quella di risonanza (ω/ω_n=1 nel grafico) si ha la risonanza e l’intensità della vibrazione diventa infinita teoricamente.

Un’ultima cosa importante da notare prima di concludere è il fatto che non abbiamo mai considerato la presenza dell’attrito. È chiaro, però, che tutti i sistemi reali hanno una certa capacità di dissipare energia. Infatti, in un caso reale dove l’effetto dell’attrito non è trascurabile non si ha uno spostamento infinito durante la risonanza, anzi, in alcuni casi la risonanza non può nemmeno avvenire. Per questo motivo lo studio delle vibrazioni meccaniche in infrastrutture critiche come un ponte non può essere trascurato al fine di garantire la sicurezza del suo utilizzo.

Articolo a cura di Axel Baruscotti