La bizzarra morte del presidente degli USA che dimostrò il Teorema di Pitagora
Teorema di Pitagora – Il 2 luglio del 1881, alla stazione ferroviaria di Washington, il 20° presidente degli Stati Uniti, James A. Garfield, fu raggiunto da due proiettili sparati da un attentatore, Charles Guiteau. Una pallottola procurò un semplice graffio ad un braccio, mentre l’altra si conficcò nel pancreas. I medici, però, non potevano saperlo, poiché all’epoca non era possibile guardare nella pancia di un paziente senza aprirla.
Il proiettile era stato deviato da una costola e quindi non c’era modo di determinarne la posizione a partire dal foro di entrata. Alexander Graham Bell, uno degli inventori del telefono, si offrì come esperto e propose l’utilizzo di un apparecchio costituito da un elettromagnete a batteria e una piccola bobina connessa ad un ricevitore telefonico. Grazie alla corrente fornita dalla batteria, veniva generato un campo magnetico costante.
Introducendo la bobina in direzione perpendicolare al campo, si potevano individuare eventuali cambiamenti del campo medesimo, perché una variazione di campo magnetico induceva una corrente nella bobina che sarebbe stata segnalata dal trillo del ricevitore telefonico. Bell pensava che, passando il dispositivo sopra il corpo di Garfield, la pallottola avrebbe modificato in qualche modo il campo magnetico, e che il ricevitore l’avrebbe rivelato.
Il fallimento dell’esperimento e la morte di Garfield

Purtroppo, il proiettile era di piombo, materiale che altera il campo magnetico in modo troppo debole per essere rivelato (l’acciaio, ad esempio, sarebbe stato decisamente meglio). Inoltre, era troppo in profondità nell’organismo. A complicare le cose e a rendere inefficace il metal detector di Bell, ci si misero pure le molle metalliche del letto del presidente. Dopo numerosi tentativi fallimentari, Bell rinunciò. Garfield morì di setticemia due mesi dopo l’attentato.
Ad estrarre il proiettile dal corpo di Garfield ci si misero ben sei dottori. William Bliss infilò le dita non lavate nella ferita ed una sonda non sterile nel tentativo di recuperare la pallottola. Un medico militare inserì nella ferita il suo dito sporco e la medesima cosa fece un altro, però quest’ultimo lo fece in modo così violento da perforare il fegato. L’attentatore disse ironicamente che a uccidere Garfield erano stati i medici e non lui. In effetti, l’autopsia dimostrò che se i dottori avessero lasciato la pallottola al suo posto, cioè vicino ad una vertebra, probabilmente il presidente sarebbe sopravvissuto.
La dimostrazione di Garfield del Teorema di Pitagora
Nel 1876, Garfield pubblicò sul “New English Journal of Education” una nuova dimostrazione del teorema di Pitagora (estremamente semplice e riportata in figura) osservando che “era qualcosa su cui i membri di entrambe le Camere potevano dirsi d’accordo, a prescindere dalle idee politiche”. Capite così il motivo per cui Garfield è passato alla storia oltre che per la estrema brevità del suo mandato presidenziale, per il fatto di essere stato un uomo che al pentagono ha preferito… il triangolo.
“Si ruoti di 90° in senso orario l’ipotenusa BC del triangolo rettangolo ABC ottenendo il triangolo rettangolo isoscele BCE. Dal punto E si conduca la perpendicolare alla retta passante per A e C e si denoti con D il suo punto di intersezione con la retta stessa. E’ immediato verificare che i due triangoli rettangoli ABC e CDE sono congruenti (hanno congruenti l’ipotenusa per costruzione e gli angoli ABC e DE in quanto complementari del medesimo angolo ACB).
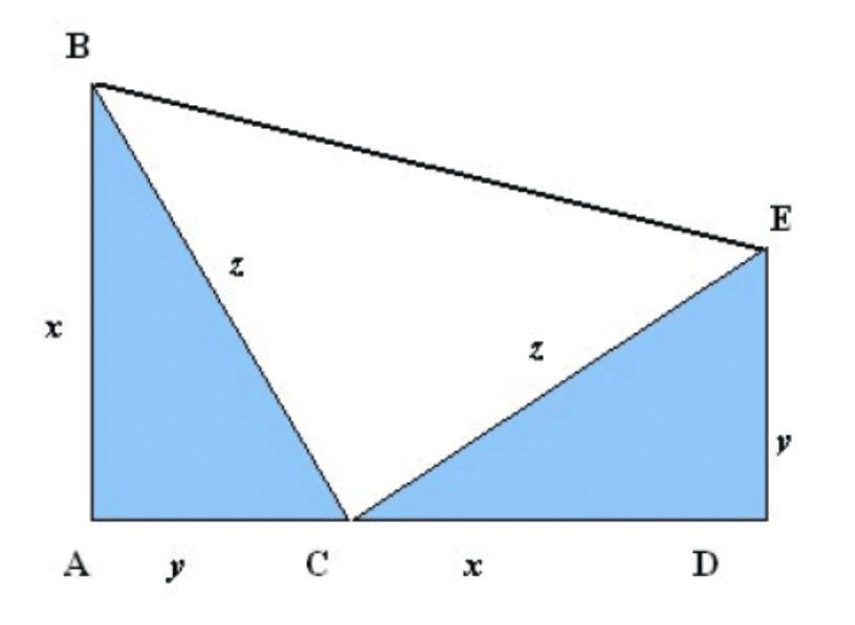
Indichiamo con x, y, z le misure dei due cateti e dell’ipotenusa. L’area A del trapezio rettangolo ADEB può essere calcolata in due modi: come semiprodotto della somma delle basi (x + y) per l’altezza (x + y) e come somma delle aree dei tre triangoli rettangoli ABC, CDE e BCE. Dunque, poiché i due triangoli rettangoli ABC e CDE hanno area xy/2 mentre il triangolo BCE ha area z2/2, ne segue che:
Uguagliando le due espressioni, si ottiene:
