Francesco Bulli, qual è la reale valenza matematica della sua scoperta?

Francesco Bulli, il ragazzo divenuto famoso per la formula del segmento parabolico
Si sa, la matematica è materia oscura ai più. Molti si scoraggiano, fin da piccoli, dinanzi ai problemi numerici più disparati, ritenendo la materia poco utile a fini pratici. Non è il caso di Francesco Bulli, sedicenne liceale di Monfalcone, che ha affrontato in maniera originale un noto problema di geometria analitica, estrapolando una formula diretta, semplificando del tutto i calcoli necessari per arrivare alla soluzione.
La notizia è rimbalzata da giornali locali, fino alle maggiori testate giornalistiche nazionali, che rendono omaggio al ragazzo, che avrebbe inventato una nuova formula per risolvere tale problema. Se da un lato l’ingegno e l’intelligenza di Bulli sono fuori discussione, che valenza ha la sua “scoperta” dal punto di vista prettamente matematico?
Il problema in esame
Il problema che la docente aveva sottoposto è un classico problema di geometria piana: determinare l’area compresa fra un arco di parabola e una retta intersecante la parabola stessa. Si tratta di un problema decisamente più complicato di quello riguardante il calcolo dell’area di poligoni regolari. In questo caso si ha a che fare con curve posizionate in maniera casuale nello spazio bidimensionale, e per questo richiede analisi più approfondite.
La soluzione classica: il teorema di Archimede
Gli oggetti in gioco sono parabola e retta, le cui espressioni analitiche sono rispettivamente $$y = ax^2 + bx + c$$ e $$y = mx + q.$$
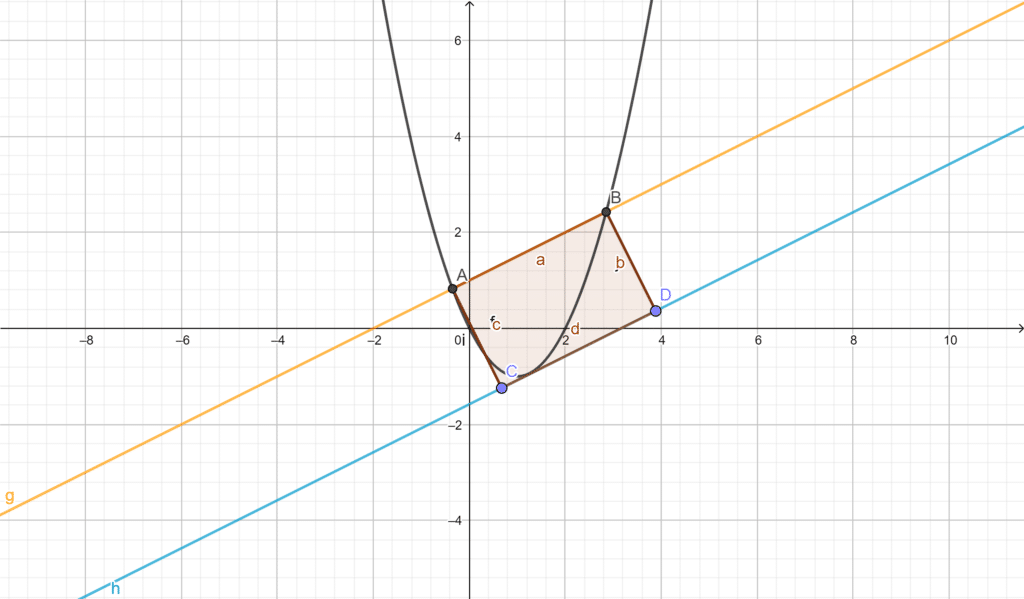
Si consideri l’immagine sopra riportata. Si vuole determinare l’area del segmento parabolico sotteso dalla retta passante per i punti A e B. Tale problema viene risolto dal famoso teorema di Archimede, che asserisce che l’area dipende dall’area del rettangolo costruito a partire dalla retta parellela a quella di partenza. Definendo la distanza tra la retta arancione e quella azzurra, si identifica un rettangolo regolare \(ABCD\).
Sia \(A_{p}\) l’area del segmento parabolico e sia \(A_{r}\) l’area del rettangolo. Allora $$A_p = \dfrac{2}{3}A_r.$$ Il teorema quindi fornisce una relazione fondamentale fra le due aree: se si conosce l’area del rettangolo, si può risalire all’area del segmento parabolico.
Tuttavia tale approccio richiede il calcolo analitico dei punti di intersezione fra prima retta e parabola, poi la definizione della retta tangente alla parabola, e poi il calcolo delle distanze fra i quattro punti \(ABCD\) per determinare l’area del rettangolo. Questi passaggi possono portare via parecchio tempo, con alta probabilità di errore di calcolo da parte anche dello studente più attento.
Una formula più diretta
Esiste però una formula più immediata, che sfrutta le proprietà di invarianza rispetto alla traslazione del sistema retta-parabola. In soldoni, si traslano entrambe facendo coincidere il vertice della parabola con l’origine degli assi cartesiani, in modo tale da semplificare al massimo l’equazione della stessa, che diventa $$y = ax^2$$ ovvero la curva è descritta semplicemente dal parametro \(a\), senza bisogno di utilizzare \(b\) e \(c\). La formula è la seguente $$A_{p} = \dfrac{1}{6} |a| |x_1-x_2|^3$$ ove \(x_1,x_2\) sono le ascisse dei punti di intersezione fra retta e parabola.
Arrivati a questo punto, il problema consiste nel trovare i due punti e il gioco è fatto. Determinare i due punti è piuttosto banale: basta imporre la condizione per cui retta e parabola si incontrano, ovvero $$y_{p} = y_{r} \rightarrow ax^2+bx+c-mx-q = 0.$$ Si riconosce subito una semplice equazione di secondo grado, le cui due soluzioni costituiscono proprio le due coordinate cercate.
Il contributo di Francesco Bulli
L’apporto dato da Bulli è semplicemente quello di ampliare la formula precedentemente vista, andando a parametrizzare la quantità \(x_1 – x_2\). Si tratta di semplici passaggi algebrici, che non richiedono particolare estro e genialità. Infatti, considerando l’equazione di secondo grado $$ax^2+bx+c-mx-q = 0$$ si procede al calcolo del discriminante $$\Delta = (b-m)^2 – 4a(c-q).$$ Tale quantità è per ipotesi strettamente maggiore di zero, dato che la retta interseca la parabola in esattamente due punti. Se così non fosse, il problema non ammeterebbe soluzione, e, in caso di retta tangente, l’area del segmento parabolico sarebbe banalmente \(0\).
Si perviene dunque alla soluzione $$x_{1,2} = \dfrac{(m-b) \pm \sqrt{\Delta}}{2a}.$$ Ora, sostituendo \(x_{1,2}\) alla formula generale di cui sopra, si ottiene, dopo banali semplificazioni $$A_{p} = \dfrac{\sqrt{[(b-m)^2 – 4a(c-q)]^3}}{6a^2}.$$
Abbiamo dunque ottenuto una formula diretta che ci consente di risolvere il problema in esame conoscendo semplicemente i parametri di parabola e retta, senza aver bisogno di ricorrere a procedimenti lunghi e noiosi.
La reale valenza del lavoro di Bulli
Come spiegato, il lavoro di Bulli non ha particolare rilevanza matematica, anche perché i problemi di area sono risolti in via immediata tramite il calcolo integrale, che il ragazzo di terza liceo ancora non conosce. Altresì, egli non ha individuato alcuna nuova formula, poiché la sua equazione non è altro che una parametrizzazione di una formula nota da tempo. In sostanza, Francesco Bulli ha dimostrato come sia possibile calcolare l’area di un segmento parabolico direttamente dai valori numerici delle equazioni delle due curve.
Mentre da un lato tale formulazione non riveste particolare importanza scientifica, dall’altro lato va riconosciuto a Bulli l’impegno, l’ingegno e la passione per una disciplina ricca di mistero e di poesia, spesso trascurata ingiustamente dai suoi coetanei e dal sistema scolastico.
