L’ipotesi di Riemann, il più grande mistero della matematica
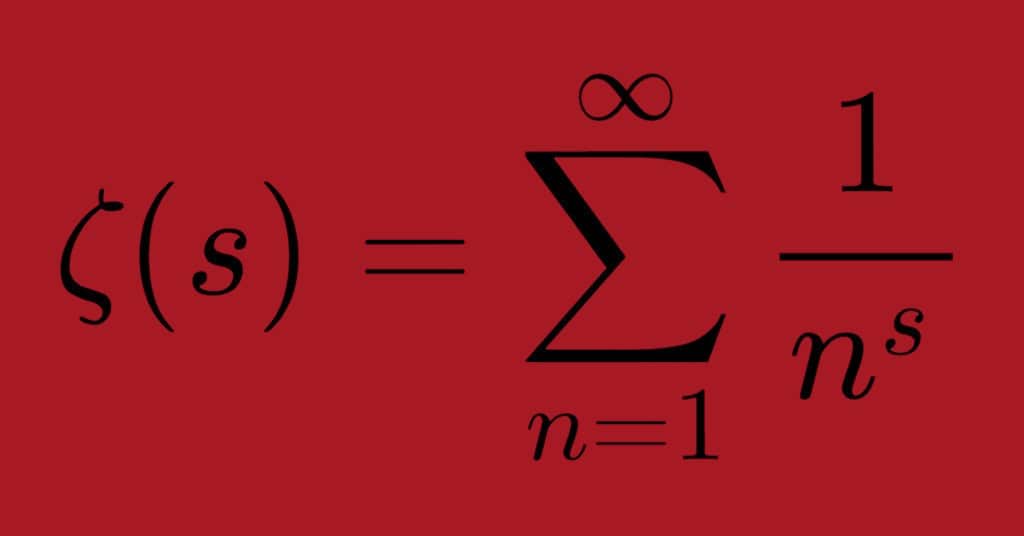
La funzione zeta di riemann
Se si parla di matematica, non si può non citare l’ipotesi di Riemann. Essa costituisce il più grande problema aperto della scienza dei numeri. Formulata nel 1859 dal matematico tedesco Georg Frederich Bernhard Riemann, questa ipotesi è strettamente connessa con la distribuzione dei numeri primi nella grande famiglia dei numeri naturali. Ma in cosa consiste esattamente questa famosa ipotesi?

Credits: wikipedia.org
L’uguaglianza di Eulero
Per comprendere l’importanza dell’ipotesi di Riemann, bisogna considerare innanzitutto i risultati di Eulero, che aveva già studiato le serie di funzioni, trovando un’uguaglianza fondamentale. Tale equazione lega una serie di funzioni ai numeri primi. In particolare, Eulero chiamò questa serie “zeta”: $$\zeta(x) = \sum_{n=1}^\infty \frac{1}{n^x} = \prod_{p \, primo} \frac{1}{1-p^{-x}} \quad , \quad x>1$$
L’estensione al campo complesso
L’intuizione geniale di Riemann fu di estendere l’argomento della funzione zeta al campo dei numeri complessi, numeri immaginari formati da multipli di \(i\), ove \(i\) è tale che \(i^2 = -1\). Il matematico tedesco iniziò a studiare questa funzione coi metodi complicati dell’analisi complessa, per capirne meglio le proprietà.
Zeri banali e zeri non banali
In particolare Riemann intraprese il viaggio negli zeri della funzione zeta, ovvero i valori di \(s\), ove \(s\) è complesso, per cui valga \(\zeta(s) = 0\). Trovò immediatamente che tale funzione si annulla per \(s = -2 , -4 , -6\) e così via. Tali valori prendono il nome di zeri banali. Scoprì poi l’esistenza di altri zeri, molto più interessanti dei primi, che egli chiamò zeri non banali. Riemann congetturò che questi zeri abbiano tutti parte reale \(\dfrac{1}{2}\).
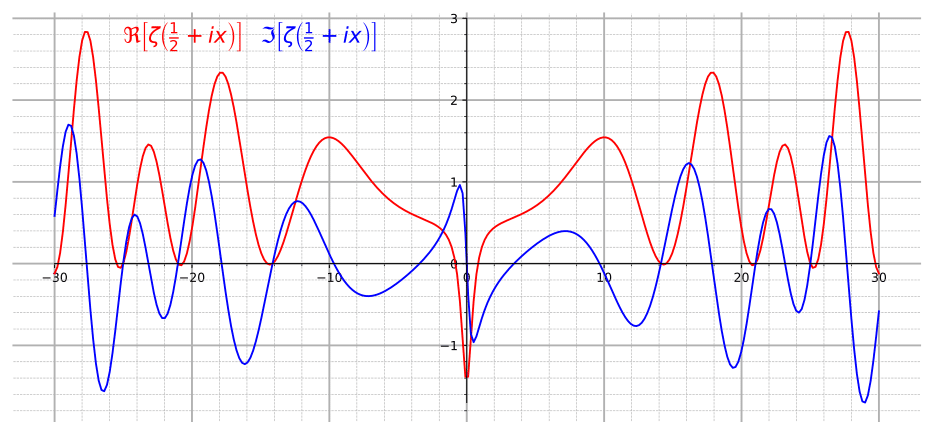
Cosa hanno in comune gli zeri della zeta e i numeri primi?
Non è semplice capire il legame fra l’ipotesi di Riemann e i la distribuzione dei numeri primi. Per dare un’idea generale, si può dire che gli zeri della funziona zeta sono le frequenze che determinano la funzione sinusoidale che esprime l’errore che si commette nell’approssimare il numero di primi in un intervallo con la funzione proposta da Gauss, ovvero \(\pi(x) \approx \frac{x}{ln(x)}\). In parole povere, dimostrare l’ipotesi di Riemann significa fornire la chiave di lettura definitiva per comprendere la musica dei primi.
L’importanza del problema
Dimostrare l’ipotesi di Riemann avrebbe delle ricadute enormi nel mondo della matematica odierna. Innanzitutto tutti i (presunti) teoremi che iniziano con
Si supponga che l’ipotesi di Riemann sia vera…
sarebbero automaticamente veri e dimostrati. Inoltre, si aprirebbero nuovi studi per migliorare la comprensione della distribuzione dei primi, per non parlare delle ripercussioni nel mondo della crittografia, dove alcuni algoritmi si basano sulla difficoltà di trovare i due fattori primi di un numero spropositatamente grande.
Il premio da un milione di dollari
Per via della sua portata, l’ipotesi di Riemann è stata inserita dall’Istituto Clay nella lista dei 7 problemi del millennio. Se qualcuno dimostrerà che essa è vera, riceverà un premio da 1 milione di dollari. Ad oggi molti matematici hanno affermato di averla dimostrata, ma puntualmente tali dimostrazioni risultavano erronee, dopo essere poste al vaglio degli esperti.
Nell’attesa che qualcuno sciolga questo nodo secolare, rimane un alone di mistero su uno dei problemi più affascinanti della storia della matematica.
