L’equazione dell’amore (che tutti sbagliano!)
Nell’era dei social network ad ognuno di voi sarà capitato di imbattersi in una conversazione fra fidanzati che inizia, più o meno, così: “Dimmi qualcosa di bello” – disse lei. “(∂ + m) ψ = 0” – rispose lui..
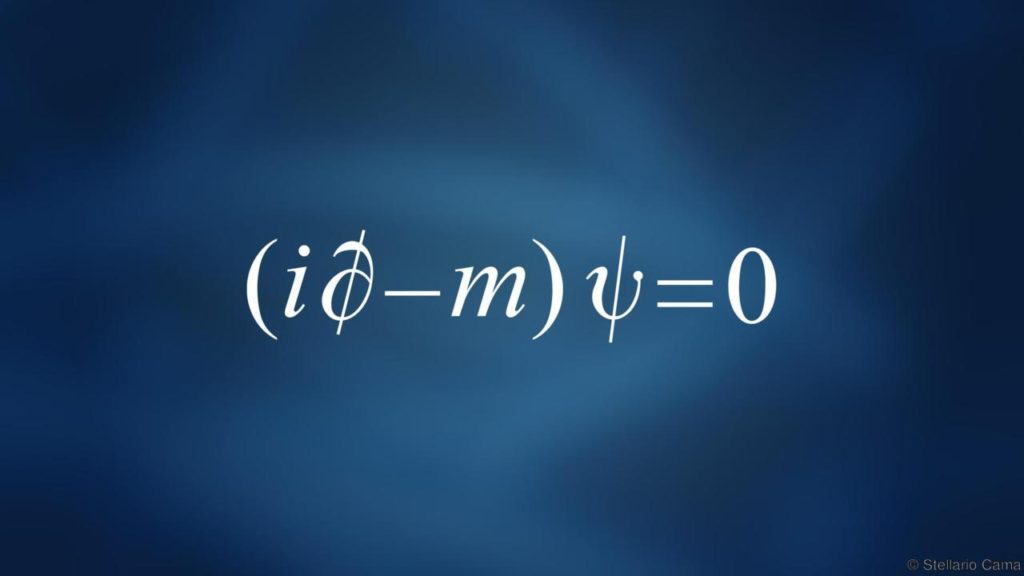
Equazione di Dirac, credits: http://ichef.bbci.co.uk/wwfeatures/wm/live/1280_720/images/live/p0/3f/y2/p03fy2zq.jpg
Nell’era dei social network ad ognuno di voi sarà capitato di imbattersi in una conversazione fra fidanzati che inizia, più o meno, così:
“Dimmi qualcosa di bello” – disse lei.
“(∂ + m) ψ = 0” – rispose lui.
“L’equazione sopra è quella di Dirac ed è la più bella equazione conosciuta nella fisica – dice un post su Instagram – Grazie a questa si descrive il fenomeno dell’entanglement quantistico, che in pratica afferma che: “Se due sistemi interagiscono tra loro per un certo periodo di tempo e poi vengono separati, non possiamo più descriverli come due sistemi distinti, ma in qualche modo sottile diventano un unico sistema. Quello che accade a uno di loro continuare ad influenzare l’altro, anche se distanti chilometri o anni luce”.

L’equazione di Paul Dirac rappresenta l’energia di una particella elementare. Viene utilizzata per le particelle di spin ½, come ad esempio gli elettroni e i quark: Dirac la formulò nel 1928 alla “tenera” età di venticinque anni. Lo scopo di Dirac era quello di ovviare agli inconvenienti generati dall’equazione di Klein-Gordon la quale mostra difficoltà nell’interpretazione della funzione d’onda, portando a densità di probabilità che possono essere anche negative o nulle, ammettendo inoltre soluzioni ad energia negativa.
[amazon box=”8806237101″]
Senza entrare troppo in dettagli noiosi ed accademici diciamo semplicemente che l’equazione di Dirac descrive le particelle elementari con l’ausilio di uno spinore composto da quattro funzioni d’onda (lo spinore di Dirac), naturale estensione dello spinore a due componenti non relativistico. Quella di Dirac è stata una svolta fondamentale verso la teoria unificata dei principi della meccanica quantistica e della relatività ristretta: ha permesso infatti di definire una densità di probabilità sempre consistente ed ha spiegato la struttura fine dello spettro dell’atomo di idrogeno e il fattore giromagnetico dell’elettrone.
Proprio come l’equazione di Klein-Gordon anche quella di Dirac ammette soluzioni ad energia negativa ma, contrariamente dalla prima, Dirac ipotizzò l’esistenza di un mare infinito di particelle che occupano tali stati ad energia negativa. Di seguito, con lo sviluppo della teoria quantistica dei campi, gli stati ad energia negativa furono identificati con le antiparticelle e con l’introduzione di un nuovo numero quantico (+1 per le particelle e -1 per le antiparticelle) così da risolvere i paradossi originati dall’ipotesi del mare di Dirac.
[amazon box=”8850250665″]
Cosa c’è di vero nel “postulato dell’amore”?
La forma della formula è certamente errata: occorre porre un meno davanti alla massa, la quantità immaginaria davanti alla derivata e la derivata è tagliata: (i∂̸ – m) ψ = 0. Il “taglietto” sulla derivata è di notevole importanza: non si tratta di un’equazione normale, quella di Dirac è un sistema di quattro equazioni. Dirac si accorse dell’impossibilità nello scrivere un’equazione di particelle cariche con spin come l’elettrone, che necessita di due equazioni, senza avere anche due soluzioni ad energia negativa. Per risolvere il problema Dirac pensò ad un mare di particelle, ma negli anni successivi si capì che le altre due equazioni rappresentavano il positrone, l’antiparticella dell’elettrone.
Ed il quantum entanglement? Questo ha senso solo per i sistemi microscopici. Se una particella a carica nulla decade producendo due particelle di carica opposta ciascuna delle due particelle non ha carica determinata sino a che qualcuno non la misura, dunque impossibile prima determinare l’influenza dell’una sull’altra. Senza contare il fatto che concetti quantistici come il collasso della funzione d’onda o l’entanglement non entrano affatto nella costruzione dell’equazione di Dirac: equazione valida solo per una sola particella libera di muoversi nello spazio intergalattico e che non interagisce con altri campi o particelle! Dunque questa equazione dell’amore? Possiamo paragonarla ad un errore grammaticale.
[amazon box=”8865089318″]

