Comprendere un’epidemia: cos’è il modello SIR?

E’ ormai chiaro che, con l’ultimo DPCM, un ruolo importante nell’evoluzione delle misure restrittive lo giocherà un parametro chiamato “indice \(R_t\)”. Cosa lo rende così speciale da poter dettare l’apertura o la chiusura delle singole regioni? Bisogna tenere a mente che, mai come in questo momento, il potere predittivo dei modelli matematici sta giocando un ruolo fondamentale nelle decisioni che influenzeranno tutti nei prossimi mesi.
Per capire meglio di cosa si tratta è necessario analizzare, nella sua forma semplificata, il modello SIR, ossia una serie di equazioni differenziali che descrivono l’evoluzione di una epidemia.

Differenza nelle notazioni

Molti di voi avranno notato che, ad inizio epidemia, tale parametro veniva indicato con \(R_0\). La differenza è che quest’ultimo viene usato per descrivere modelli di epidemia non forzata, ovvero senza misure restrittive. Poiché, invece, in Italia sono in vigore ormai da settimane severe disposizioni limitative, è stato deciso di chiamare il parametro \(R_t\). Nel corso della trattazione, poiché il modello considerato è non forzato, sarà adottata la notazione \(R_0\).

Le equazioni differenziali

Prima del modello vero e proprio è necessario chiarire una cosa: Che cos’è un’equazione differenziale?
In generale quando incontriamo un’equazione algebrica siamo di fronte ad una formulazione matematica in cui ci chiediamo “qual è il numero che sostituito alla \(x\) rende un’uguaglianza vera?”. Un classico esempio di modello algebrico è il seguente: $$3x + 2 = 5.$$

Per quanto concerne un’equazione differenziale, la domanda risulta essere molto simile ma, in questo caso, invece di una serie di numeri (scalari) vogliamo trovare una funzione che soddisfi un’uguaglianza.
In un’equazione differenziale vengono messe in relazione tra loro le derivate di una funzione incognita con la funzione stessa, insieme ad una serie di opportune condizioni iniziali.
Cos’hanno di speciale le equazioni differenziali? Ogni fenomeno fisico è descritto da un’equazione differenziale più o meno complessa, a partire da una sfera che cade verso il basso, passando per il moto di una foglia lungo un corso d’acqua e arrivando al tempo che impiega un certo farmaco a diffondersi nel sangue.

Di seguito un esempio di equazione differenziale ordinaria del secondo ordine: $$\begin{split} \dfrac{d^2y}{dt^2} + a \, \dfrac{dy}{dt} – by & = f(t) \\ y(t_0)&=y_0 \\ y'(t_0)&=y’_0.\end{split}$$

Il modello SIR

Il modello base da cui si parte per descrivere l’andamento di un’epidemia è il SIR, dove la sigla sta a significare : “Suscettible, Infected, Recovered”.

Questa serie di equazioni, infatti, considera l’esistenza di tre tipologie di persone:

• Chi non si è ammalato;
• Chi è attualmente malato;
• Chi è guarito oppure morto.

Le principali assunzioni di questo modello sono che queste tre categorie siano sufficientemente mescolate tra loro (dunque non tiene in considerazione la possibilità di isolare gli infetti) e che, una volta guariti, non sia possibile ammalarsi nuovamente.
Queste assunzioni semplificative servono a rendere più accessibile la soluzione ma, contemporaneamente, vanno a discapito della sua efficacia predittiva. Nello specifico il modello è il seguente: $$\begin{split} \dfrac{dS}{dt} & = -\beta SI \\ \dfrac{dI}{dt} & = \beta SI – \gamma I \\ \dfrac{dR}{dt} & = \gamma I. \end{split}$$

La prima equazione del modello SIR

La prima equazione risponde alla seguente domanda: “come varia il numero di pazienti suscettibili nel tempo?”. Possiamo notare che è presente il termine \(-\beta SI\), questo significa che i pazienti suscettibili diminuiscono nel tempo in proporzione al prodotto dei suscettibili per gli infetti. In altre parole, come faccio a far ammalare una persona suscettibile all’infezione? Devo avere almeno un infetto ed almeno una persona suscettibile (infatti se \(I=0\) o \(S=0\) questo termine di variazione diventa nullo) e, in aggiunta, questo tasso di infezione avrà un certo coefficiente di proporzionalità \(\beta\) che è una caratteristica della specifica infezione.

La seconda e la terza equazione

La seconda equazione esprime la variazione del numero degli infetti. Questa volta abbiamo due termini:
uno che aumenta il numero degli infetti (\(\beta SI\)), ed uno che tende a farlo diminuire (\(\gamma I\)). Per quanto riguarda il termine additivo il discorso è lo stesso di prima, il termine sottrattivo invece è legato alla capacità di un infetto di guarire.

Il numero di guariti sarà dunque proporzionale al numero di persone attualmente infette moltiplicato per un coefficiente \(\gamma\) che può essere interpretato come un tempo caratteristico di guarigione.
Anche in questo caso notiamo una cosa (per altro abbastanza intuitiva): se il numero di infetti è nullo allora il tasso di guarigione sarà zero essendo pari a \(\gamma I\).

La definizione del parametro \(R_0\)

A questo punto abbiamo gli strumenti per definire il nuovo parametro $$R_0 = \dfrac{\beta N}{\gamma},$$ dove il prodotto \(\beta N\) è il numero di infezioni che può causare un singolo infetto su una popolazione di \(N\) individui, mentre \(\dfrac{1}{\gamma}\) è l’inverso del tempo caratteristico del periodo di infezione.

Possiamo interpretare questo indice, dunque, come “il numero di infezioni che un singolo individuo può produrre durante il periodo in cui egli è potenzialmente infettivo”. Ci si può rendere immediatamente conto dell’importanza di questo valore. Usando dei dispositivi di protezione, aumentando le nostre norme igieniche e distanziandoci possiamo far sì che $$R_0 < 1.$$Sotto questa condizione è possibile far regredire l’epidemia.

C’è di meglio all’orizzonte?

Quali sono i limiti di questo modello appena discusso? In primo luogo abbiamo fatto alcune ipotesi semplificative che, seppur siano utili alla risoluzione dell’equazione, rendono il risultato meno accurato oltre un certo range.

Esistono sistemi di equazioni differenziali notevolmente più realistici ma che, purtroppo, risultano anche più complessi da gestire. Un primo esempio di modello più accurato è il SIRS nel quale viene aggiunta la possibilità che una persona guarita sviluppi un’immunità solo per un certo arco di tempo e che, dunque, possa riammalarsi.

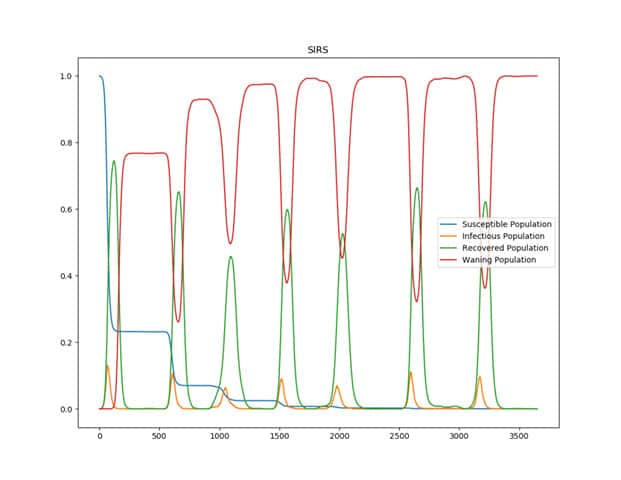
È necessario, in genere, un continuo lavoro di confronto tra predizione teorica e dati sperimentali in modo da modificare i parametri nel tempo per ottenere, volta per volta, un risultato accurato.
Modelli come il SIR o simili ci forniscono dei risultati validi e validabili in un determinato arco temporale. In una situazione delicata come quella in cui stiamo vivendo, la matematica ci permette di non brancolare nel buio e di teorizzare le necessarie misure preventive.

Articolo a cura di Carmine Schiavone.