Quando la matematica ti fa vincere un’auto nuova

La matematica è la scienza che permea la realtà di ogni giorno, tuttavia spesso può risultare controindicativa, come dimostra il famoso paradosso di Monty Hall. Tale paradosso saltò fuori in un celebre gioco a premi americano, “Let’s make a deal”, condotto da Maurice Halprin, il cui pseudonimo era appunto Monty Hall.

Il gioco del quiz televisivo

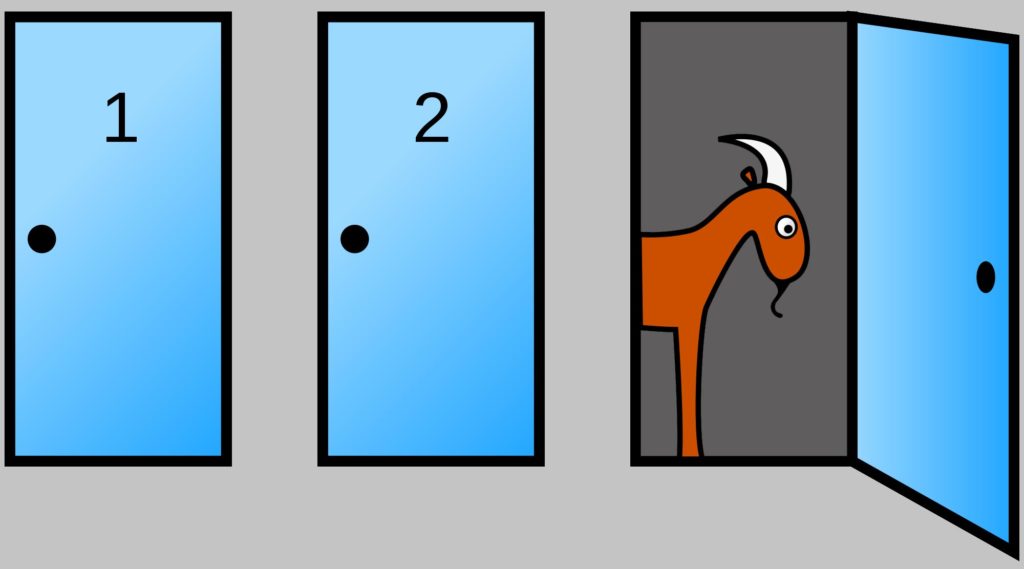
Il gioco è molto semplice: il giocatore ha davanti a sé tre porte chiuse. Dietro una di queste si cela un’automobile, mentre dietro le altre due sono nascoste due capre. Il conduttore di quiz televisivo chiede al concorrente di scegliere una porta, e il giocatore opta ad esempio per la porta 3. A questo punto, il conduttore – che sa cosa c’è dietro le porte – ne apre un’altra (la 1 o la 2) svelando dietro di essa una capra. Ora egli chiede al giocatore se intende cambiare porta oppure no.

Gli approcci intuitivi ed erronei

Ed è proprio qui che entra in ballo la matematica. Uno potrebbe essere portato a pensare di avere il 50% di probabilità, essendo rimasti una capra e l’automobile. O ancora potrebbe sospettare che il conduttore stia cercando di sviarlo per farlo perdere. Tuttavia queste sono associazioni erronee che non tengono conto della cosiddetta probabilità condizionata.

Le probabilità raddoppiano!

All’inizio il concorrente ha probabilità 1/3 di vincere l’auto. Tuttavia il fatto che il conduttore apra un’altra porta con dietro una capra sta di fatto cambiando lo scenario del gioco, aggiungendo un’informazione essenziale al concorrente. Infatti, cambiando porta, il giocatore vince l’auto con probabilità 2/3. In pratica le probabilità di vincere raddoppiano. Ma com’è possibile? Ciò appare chiaro analizzando tutti I possibili casi che si presentano al giocatore rimasto con sole due porte:

1. Dietro la porta scelta in partenza c’era l’automobile. Il giocatore cambia e perde.

2. Dietro la porta scelta in partenza c’era la capra numero 1. Il giocatore cambia e vince.

3. Dietro la porta scelta in partenza c’era la capra numero 2. Il giocatore cambia e vince.

Citando i latini, tertium non datur. Come si evince dal ragionamento, il giocatore vince in due casi su tre, qualora decida di cambiare porta. La natura controindicativa di questo gioco risiede nel fatto che spesso pensiamo che il passato non influenzi il presente da un punto di vista probabilistico.

Il paradosso nella settima arte

Il gioco viene proposto anche nel film 21, diretto da Robert Luketic. Il professore di matematica Mickey Rosa (intepretato da Kevin Spacey) lo sottopone ad un suo studente, che lo risolve brillantemente in pochi secondi, ricorrendo proprio alla probabilità condizionata, altrimenti detta metodo del cambio di variabile.

Questo paradosso è l’esempio di come sia facile confondere la psicologia e la matematica: un concorrente potrebbe pensare che il conduttore stia cercando di truffarlo chiedendogli se vuole cambiare porta. Tuttavia non c’è alcun sotterfugio: basta ricorrere alla matematica per vincere un’auto nuova di zecca!