Perché l’area del cerchio di raggio r è pari a πr²?

L’area del cerchio di raggio r è pari a πr². Perché? Una strategia per dimostrarlo consiste nell’immaginare il cerchio come una pizza, per poi dividerla in un’infinità di fette, da riordinare opportunamente fino a formare un rettangolo: questo ci fornirà la risposta, perché lo spostamento delle fette non modifica l’area iniziale e sappiamo come calcolare l’area di un rettangolo, cioè moltiplicando la misura della sua base per quella della sua altezza.
Perché l’area del cerchio di raggio r è pari a πr²? Immaginiamo due pizze ideali
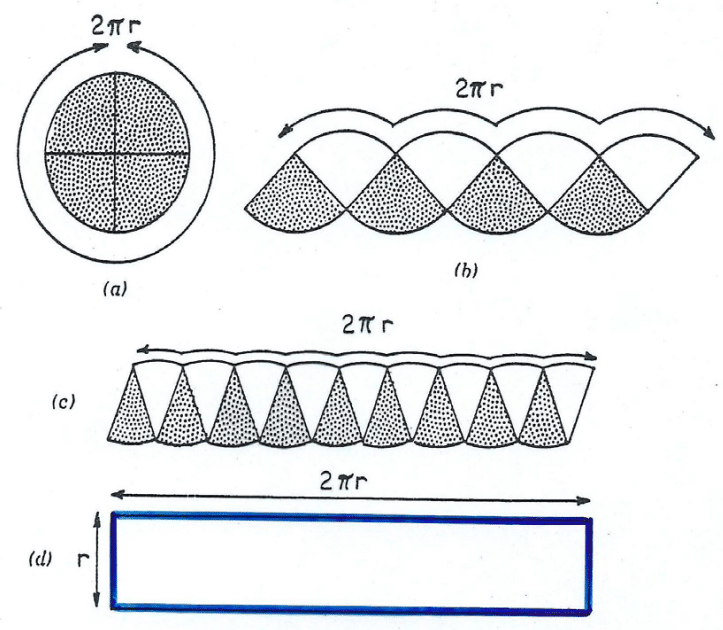
Ad essere precisi, la pizza deve essere una pizza matematica idealizzata, perfettamente piana e circolare, con una crosta infinitamente sottile. Immaginate, dunque, di avere due pizze delle stesse dimensioni (raggio r), come nella figura A qui sopra (una è stata evidenziata in bianco e l’altra con dei puntini neri). La circonferenza di queste pizze è pari a 2πr.
Cominciamo col suddividere ciascuna pizza in quattro fette uguali e col disporle come in figura B (alternando fette grigie e fette bianche). La curiosa forma dentellata che si viene a formare, naturalmente, ha l’area pari alla somma delle aree dei due cerchi, sebbene la cosa non sembri molto utile, dato che non conosciamo neppure la sua area.
Ma sappiamo almeno due cose importanti su di lei. Primo: i quattro archi alla sua base e in alto hanno una lunghezza complessiva uguale a 2πr. Secondo: i segmenti ai lati sono lunghi r, dal momento che ognuno di loro era originariamente un raggio del cerchio.
Un procedimento che va all’infinito

Ora ripetiamo il medesimo procedimento, ma questa volta con dieci fette, riassemblate in modo alternato, come in figura C. La forma dentellata appare, adesso, meno strana. Gli archi in alto e in basso (in tutto dieci) sono tuttora presenti, ma risultano meno pronunciati; i lati destro e sinistro sono meno inclinati di prima. E continuano a valere, nonostante questi cambiamenti, i due fatti di prima: gli archi alla base e in alto hanno una lunghezza complessiva pari a 2πr e ogni lato è ancora lungo r.
Inoltre, la sagoma continua ad avere la stessa area di prima, dal momento che è solo una riorganizzazione delle venti fette di pizza. Aumentando il numero di fette, accade una cosa straordinaria: la sagoma dentellata tende a diventare un rettangolo: gli archi si appiattiscono e i lati diventano quasi verticali. Nel limite di infinite fette, la sagoma è un rettangolo (figura D).
Come prima, continuano a valere quei due fatti, per cui questo rettangolo ha la base lunga 2πr e l’altezza r. Ma ora il problema è semplice! L’area del rettangolo – che è la somma delle aree delle due pizze – è 2πr², per cui l’area di una pizza è πr².
Questo procedimento al limite che porta ad immaginare infiniti pezzi, ciascuno infinitesimamente piccolo, è l’idea chiave alla base di tutto il calcolo inifinitesimale: in ogni passo del procedimento la sagoma dentellata ha un aspetto bizzarro e poco incoraggiante, ma quando la portiamo al limite, quando giungiamo al traguardo, diventa semplice e bella, e tutto diviene più chiaro.
All’infinito tutto diventa più facile.
Immagine di copertina generata con DALL-E
