Il problema dei tre corpi: in cosa consiste “il più celebre di tutti i problemi dinamici”?

Nella meccanica celeste, il problema dei tre corpi è uno degli enigmi più affascinanti, e una sfida matematica e fisica di lunga data. Questa questione, descritta per la prima volta in termini moderni da Edward Whittaker come “il più celebre di tutti i problemi dinamici”, indaga il movimento di tre corpi puntiformi che si attraggono mutualmente secondo la legge universale di gravitazione di Newton.

Un problema di vasta portata: il movimento celeste e le sue infinite configurazioni

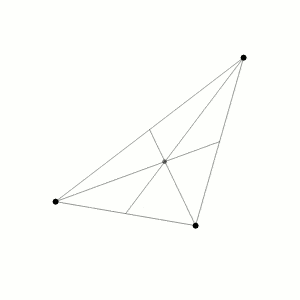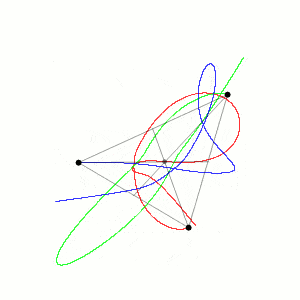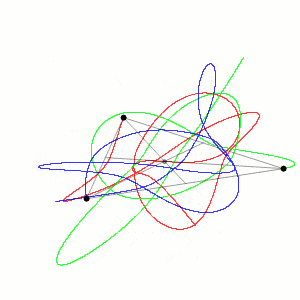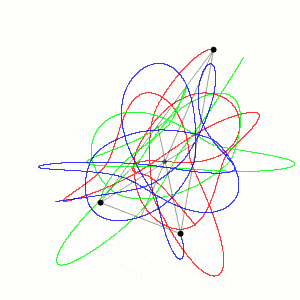
“Il problema dei tre corpi, definito da Whittaker “the most celebrated of all dynamical problems”, si enuncia come segue: Tre masse puntiformi, libere di muoversi nello spazio, si attraggono reciprocamente secondo la legge newtoniana di gravitazione. Si chiede di determinarne il movimento per qualunque configurazione e velocitè iniziale.”

Al cuore del problema dei tre corpi giace una domanda apparentemente semplice ma profondamente complessa: come si muovono tre corpi celesti sotto l’influenza reciproca della gravitazione universale, data una loro configurazione iniziale e le rispettive velocità? Questo quesito, a prima vista circoscritto, rivela in realtà una portata universale e applicazioni che si estendono ben oltre il contesto astronomico immediato.

Il problema dei tre corpi ha radici profonde nella meccanica celeste, una disciplina che studia i movimenti dei corpi celesti nello spazio sotto l’effetto della gravità. Questo problema, formulato nell’ambito della legge di gravitazione universale di Newton, si concentra sulle interazioni dinamiche tra tre corpi, quali possono essere pianeti, stelle o satelliti, cercando di prevedere le loro traiettorie in base alle condizioni iniziali.

Dai pianeti agli asteroidi: un campo di applicazione vasto

La sua vasta applicabilità spazia dalla comprensione del moto dei pianeti interni del nostro sistema solare – Mercurio, Venere, Terra e Marte – considerando l’influenza gravitazionale combinata di Giove e del Sole, fino allo studio degli asteroidi che orbitano nel nostro sistema solare, influenzati anch’essi dalla massiccia presenza di Giove. Questa questione diventa ancora più intrigante quando si considera il moto della Luna, i cui movimenti sono influenzati dalla gravità terrestre e solare, oppure quando si esplorano le dinamiche delle sonde spaziali e dei satelliti artificiali, lanciati dall’uomo nello spazio per esplorare l’universo o per fini di telecomunicazione.

Complessità e soluzioni: il “problema ristretto dei tre corpi”

Il fascino del problema dei tre corpi non risiede solo nelle sue applicazioni pratiche ma anche nella sua intrinseca complessità teorica. Nonostante siano passati secoli dalla sua formulazione, una soluzione generale e completa si è rivelata elusiva, sfidando alcune delle menti più brillanti nel campo della matematica e della fisica.

Tuttavia, sono stati fatti progressi significativi attraverso l’approccio del problema ristretto dei tre corpi, una versione semplificata in cui uno dei tre corpi ha una massa trascurabile rispetto agli altri due, e non influisce sul loro movimento. Questa semplificazione consente di ridurre la complessità dei calcoli e di esplorare situazioni specifiche con maggiore dettaglio.

Questa variante semplificata, ma non meno intrigante, è dunque il “problema ristretto dei tre corpi”, dove due corpi, detti primari, si muovono secondo orbite kepleriane fisse mentre il terzo corpo, di massa trascurabile, si muove sotto l’influenza gravitazionale dei primari senza alterarne il moto. Anche in questa configurazione semplificata, la complessità del movimento del terzo corpo, o planetoide, rimane un argomento di studio profondo.

Il problema dei tre corpi, quindi, anche nella sua versione semplificata nasconde una complessità che va ben oltre gli aspetti pratici. Il matematico francese del tardo XIX secolo, Henri Poincaré, ha elevato questa questione a un pilastro per lo sviluppo della teoria generale dei sistemi dinamici, dimostrando come possa servire da fondamento per una vasta gamma di ricerche in matematica applicata.

Perché il “problema dei tre corpi” non ha una soluzione generale?

Il problema dei tre corpi non ha una soluzione generale analitica per diverse ragioni, che affondano le radici nella natura delle equazioni differenziali che lo governano e nella complessità intrinseca dei sistemi dinamici che descrivono. Proviamo a spiegare alcuni dei motivi principali:

Non-linearità delle equazioni

Le equazioni di movimento nel problema dei tre corpi sono profondamente non-lineari. La legge di gravitazione universale di Newton stabilisce che la forza tra due corpi è proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza che li separa. Quando si aggiunge un terzo corpo, le interazioni diventano notevolmente complicate perché ogni corpo subisce la forza gravitazionale degli altri due, rendendo le equazioni del moto non lineari e interconnesse in un modo che non permette una soluzione analitica semplice.

Sensibilità alle condizioni iniziali

Il problema dei tre corpi è un esempio di sistema dinamico caotico, il che significa che è estremamente sensibile alle condizioni iniziali. Piccole variazioni nelle posizioni o nelle velocità iniziali dei corpi possono portare a differenze enormi nel comportamento del sistema nel lungo termine. Questa sensibilità rende difficile trovare soluzioni generali prevedibili e stabili per ogni possibile configurazione iniziale dei tre corpi.

Assenza di soluzioni chiusa

Henri Poincaré dimostrò che non esistono soluzioni generali sotto forma di funzioni matematiche semplici per il problema dei tre corpi. Questo significa che, a differenza del problema a due corpi, per cui esistono soluzioni esatte che descrivono orbite ellittiche secondo le leggi di Keplero, per il problema dei tre corpi non è possibile esprimere le soluzioni in termini di funzioni elementari o serie di potenze che convergono universalmente.

Approcci numerici e specifici

Sebbene non esista una soluzione generale analitica, il problema dei tre corpi può essere affrontato con metodi numerici, che forniscono soluzioni approssimate per configurazioni specifiche. Questi metodi sfruttano la potenza di calcolo dei computer per simulare le traiettorie dei corpi celesti con grande precisione, anche se richiedono un’analisi caso per caso.

Tuttavia, la complessità del “Problema dei tre corpi” ha anche spinto l’innovazione in matematica e fisica, portando allo sviluppo della teoria del caos e migliorando la nostra comprensione dei sistemi dinamici complessi.

Un’applicazione del Principio di Relatività Generale

L’interesse per il problema dei tre corpi non è limitato alla meccanica classica. Esso rappresenta anche un campo di prova per la teoria della relatività generale di Einstein, poiché offre una prospettiva diversa sulle interazioni gravitazionali e sullo studio del cosmo.

La teoria della relatività generale di Einstein, introdotta all’inizio del XX secolo, ha rivoluzionato la nostra comprensione della gravità non più come una forza a distanza, ma come una curvatura dello spaziotempo causata dalla presenza di massa ed energia. Questo cambiamento di paradigma ha aperto nuove porte per l’interpretazione e l’analisi del problema dei tre corpi, specialmente in contesti dove gli effetti gravitazionali sono estremamente forti, come nei sistemi di buchi neri o stelle di neutroni.

Nell’ambito della relatività generale, il problema dei tre corpi acquisisce nuove sfumature, soprattutto quando si considerano effetti come la precessione del perielio o la radiazione gravitazionale. Per esempio, in un sistema binario composto da due stelle di neutroni o da un buco nero e una stella di neutroni, l’aggiunta di un terzo corpo massiccio può influenzare significativamente la dinamica del sistema, causando deviazioni dalle previsioni newtoniane che possono essere calcolate solo attraverso la relatività generale.

Anche nella relatività generale, il problema dei tre corpi non ammette soluzioni analitiche semplici a causa della sua intrinseca complessità. In ogni caso, l’avanzamento tecnologico ha permesso lo sviluppo di sofisticati metodi numerici che possono simulare sistemi gravitazionalmente complessi. Questi metodi, che includono tecniche come l’analisi perturbativa e i metodi di integrazione numerica diretta, permettono agli scienziati di esplorare scenari altamente dinamici e non lineari, fornendo preziose intuizioni sul comportamento di sistemi gravitazionalmente intensi.

Il Problema dei tre corpi nella scienza fizione

Il problema dei tre corpi rimane un punto focale nella ricerca scientifica. La sua complessità e le sue sfide continuano a stimolare la curiosità e l’ingegno degli scienziati, e non solo. Il “problema dei tre corpi” ha anche ispirato la trilogia dei Tre Corpi di Liu Cixin, iniziata con Il problema dei tre corpi nel 2006 e seguita da La foresta oscura e Il finimondo. Questa saga esplora un vasto arco narrativo che va dall’incontro degli essere umani con una civiltà aliena avanzata fino alle conseguenze cosmiche di questo contatto.

Attraverso una mescolanza di fantascienza hard, filosofia e questioni etiche, la serie cinese delinea un futuro in cui l’umanità deve affrontare sfide sia interne che esterne, utilizzando la fisica e le strategie di sopravvivenza interstellare come metafore per indagare il destino dell’umanità e la natura dell’universo. Vincitrice del Premio Hugo, questa trilogia ha non solo elevato la letteratura di fantascienza cinese sulla scena mondiale ma ha anche ispirato una serie uscita da poco su Netflix, “3 body problem”.