La matematica dietro allo spettacolare crollo del Tacoma Bridge

L'inizio del crollo del Tacoma Bridge
Molti di voi sicuramente conoscono il famosissimo crollo del ponte di Tacoma Narrows, avvenuto il 7 novembre del 1940. Il ponte era all’epoca la terza struttura sospesa più lunga del mondo dopo il Golden Gate Bridge di San Francisco e il George Washington Bridge di New York.
Le cause del crollo
Il ponte presentava già oscillazioni subito dopo l’inaugurazione, ma esse divennero insostenibili per la struttura quel giorno di novembre, con il conseguente crollo di parte del ponte, che sembrava incredibilmente dondolare come un’altalena.
L’ingegnere italiano Giulio Krall fu il primo a spiegare tecnicamente la causa del crollo, affermando che una velocità del vento pari a quella di quel giorno rappresentava il valore al quale la struttura non avrebbe più potuto reggere i fenomeni di risonanza.
Il ponte come sistema dinamico
Tralasciando le complesse relazioni matematiche della scienza delle costruzioni, si può considerare il Tacoma Bridge come un generico sistema dinamico soggetto a disturbi esterni. Tradotto in parole più semplici, significa che il ponte è un oggetto il cui comportamento può essere descritto da equazioni differenziali, basate sulle leggi di Newton. In questo caso una delle leggi che si può trovare è quella fra spostamento verticale \(y\) e vento \(w\).
Il crollo spiegato matematicamente
Tale relazione matematica fra \(w\) e \(y\) ci aiuta a capire perché il ponte è effettivamente crollato. Nella teoria dei sistemi, si rappresenta questa relazione con una cosiddetta funzione di trasferimento \(T(s)\). Si tratta di una funzione polinomiale fratta, e il comportamento del sistema è determinato dalle radici dei poli al denominatore. Il Tacoma Bridge può essere modellato da una relazione del seguente tipo $$y = \frac{1}{\omega_n^2 + 2\zeta \omega_n s + s^2} w$$ ove il polinomio al denominatore ha radici complesse coniugate.
Il fattore \(\zeta\) prende il nome di smorzamento, ed è tale per cui \(\lvert \zeta \rvert\ \in [0,1]\). Degli strumenti grafici, chiamati diagrammi di Bode, determinano quanto varia l’ampiezza dell’uscita in funzione delle frequenze di ingresso. La cosa interessante è che, quando \(\zeta\) è vicina a zero, il modulo del diagramma esplode, formando la famosa risonanza.
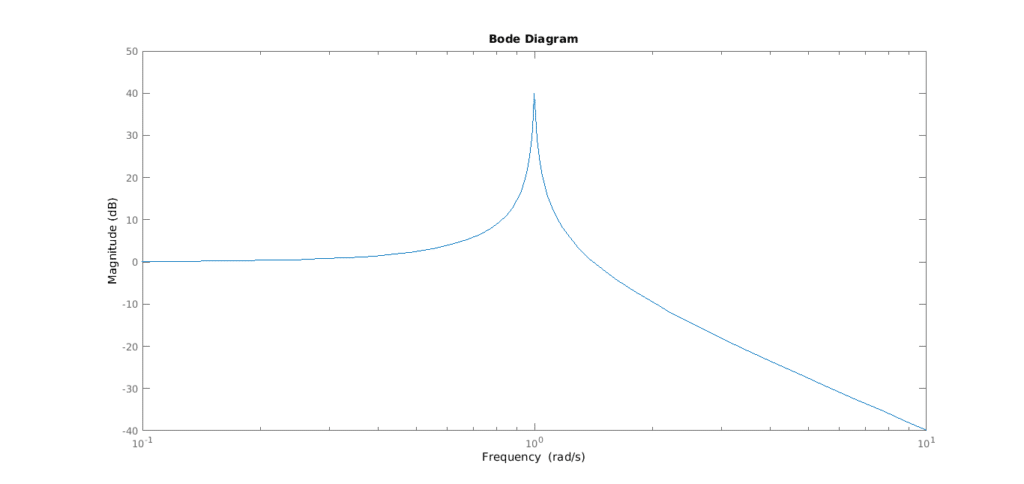
Tradotto in termini pratici, significa che i parametri fisici del ponte (che determinano le radici complesse della funzione di trasferimento) erano stati progettati malissimo, facendo quindi tendere \(\zeta\) a 0. Quindi, quando il vento raggiunge una determinata frequenza (piuttosto alta), la risonanza viene “attivata”, e lo spostamento verticale raggiunge picchi non più sostenibili dalla struttura.
La ricostruzione
Nel 1950 il ponte fu ricostruito con maggiore attenzione alla rigidezza torsionale, grazie ad una struttura a traliccio decisamente più resistente a venti ad alta frequenza. Che significa in termini matematici? Che \(\zeta\) tende ora ad 1, evitando la così tanto odiata risonanza!
