Immanenza delle nozioni di “numeri” e “matematica” nella realtà quotidiana
Può la somma dei numeri naturali fare meno un dodicesimo? Credits: triesteallanews.it
Articolo a cura di Francesca Maria Iervolino.
Paul Adrien Maurice Dirac, matematico e fisico britannico, premio Nobel per la Fisica nel 1933, considerato uno dei padri della moderna meccanica quantistica, disse: “La bellezza matematica è una qualità che non può essere definita, non più di quanto la bellezza possa essere definita per l’arte, ma chi studia matematica, di solito, non ha difficoltà ad apprezzarla”. Da quando l’uomo ha imparato a razionalizzare tutte le esperienze che vive protendendosi verso la comprensione, la conoscenza e la misura delle realtà con cui si raffronta, il concetto di numero ha assunto un ruolo sempre più profondo, affascinante e familiare per ciascun essere umano. Un amichevole sostegno per ordinare un caos che altrimenti avrebbe governato la vita sulla terra.
La matematica interpreta la realtà quotidiana
In realtà la percezione stessa di numero, questo ente seppur astratto per definizione e difficile da descrivere senza ricorrere ad un assioma cognitivo, così difficile da assoggettare ai rigidi canoni della realtà concreta della vita quotidiana, ha di per sé un ruolo, un impatto ed una influenza difficilmente quantificabili nella vita di ciascuno di noi.
I numeri scandiscono, regolano, concretizzano la nostra vita quotidiana. La mattina ci svegliamo perché la sveglia mostra che è ora di iniziare la nostra giornata. I numeri ci rassicurano con la loro imprescindibile presenza: scegliamo la temperatura dell’acqua per la doccia, del caffè, scegliamo a che velocità spostarci in auto, quando pranzare, a che ora incontrare gli amici. Stiamo utilizzando i numeri e la matematica per regolare e rendere piacevole la nostra vita, e forse non ce siamo resi conto.
Fra matematica e filosofia
Parlare di ‘immanenza’ dei numeri, enti per definizione ammissibili solo ponendo la loro esistenza come assioma naturale, nella realtà che viviamo giorno per giorno, potrebbe apparire una astrazione filosofica. Nondimeno, una scienza complessa come la matematica, ci permette di confermare in maniera logica l’esistenza di questi princìpi, tanto evidenti di per sé, da non aver bisogno di esser dimostrati. Così i numeri, di cui nessuno metterebbe in dubbio la realtà, vengono posti a fondamento di teorie deduttive, di postulati, di costruzioni cognitive più o meno complesse ed assumono di diritto un ruolo chiave nel descrivere, quantificare e qualificare la realtà che ci circonda.
Il raggiungimento dei più grandi obiettivi
La matematica ci permette di scoprire relazioni sempre più strette tra gli eventi naturali, i nostri pensieri, le nostre aspirazioni ed i numeri. Ad esempio, sarebbe inconcepibile anche per la mente umanamente più sofisticata ed evoluta, sognare e progettare un volo che ci permetta di lasciare il nostro pianeta, senza ricorrere ai concetti fondamentali di numero e di calcolo. Ma se l’uomo è stato in grado di camminare sul suolo lunare e di progettare il prossimo passo verso Marte, è stato grazie all’esistenza di una idea tanto naturale quanto immateriale: il numero. In questo modo, l’idea di immanenza non appare più tanto contemplativa ma si rivela come ‘concretezza’: una concreta presenza nella nostra vita quotidiana che garantisce stabilità e rende possibile avverare le aspirazioni umane più ingegnose. Questa immanenza diventa così una condizione della realtà che percepiamo e che possiamo misurare, quantificare, in quanto intimamente legata all’altra realtà, quella numerica. Una realtà fatta di numeri presenti in tutte le attività umane, che in gran parte rappresenta la base e la garanzia per lo sviluppo ed il progresso dell’ingegno umano. Ad usare parole più vicine alla filosofia, potremmo dire che la realtà è tale, o tale la percepiamo, perché la possiamo misurare, comprendere, grazie ai numeri.
Lo studio della matematica come affascinante scoperta
Sovente il fascino della realtà è talmente elettrizzante da soverchiare le regole stesse che lo rendono tanto avvincente. L’esempio menzionato prima ne è una prova indubitabile: quante volte si sente parlare (a scuola, tra amici o alla televisione) di concetti come la velocità, il tempo necessario a coprire una certa distanza oppure di quanto siano distanti due luoghi? E quanto spesso si sente parlare della formula matematica che rende comprensibile questo prodigio? Generalmente, il concetto di ‘numero’ è definito come ‘un modo di esprimere una quantità, oppure la posizione in un elenco di
elementi, oppure il rapporto tra grandezze dello stesso tipo’. L’idea di questo ente nasce come necessità per l’ingegno umano di misurare, contare, quantificare, descrivendo una relazione comprensibile, una corrispondenza biunivoca tra gli elementi presenti in due insiemi distinti. Per questo nasce anche il concetto di operazione numerica, ovvero quel metodo (che poi impareremo a padroneggiare come operazione aritmetica) che partendo da uno o più numeri, genera un altro numero legando questi elementi mediante un rapporto comprensibile e chiaro, quanto quello esaminato in precedenza.
Numeri, aritmetica e algebra
Una relazione algebrica lineare, abitualmente, può essere considerata come un rapporto matematico tra varie grandezze che definiamo numeri, variabili, parametri o costanti. Può svilupparsi in maniera più o meno semplice da analizzare, può prevedere legami più o meno complessi tra le grandezze coinvolte ed essere descritta con parole più o meno complesse oppure con una enunciazione semplice e lineare. Fin qui, l’aritmetica e l’algebra dei naturali sono di per sé espresse e descritte in maniera completa, e soprattutto comprensibile alla maggioranza dei discenti.
Fra matematica e fisica
Per un attimo si pensi ad una relazione algebrica del tipo: v = s / t. Ovvero: la velocità (v) è uguale alla distanza (s) divisa per il tempo (t). Tre semplicissime grandezze con cui tutti noi ci confrontiamo tutti i giorni: velocità, spostamento e tempo. Queste grandezze vengono mostrate in una relazione algebrica estremamente semplice da comprendere e che prevede una sola operazione aritmetica di base. Le quattro operazioni numeriche fondamentali ci permettono di comprendere chiaramente questa meccanica delle grandezze fisiche e l’aritmetica rappresenta proprio lo studio delle proprietà di queste operazioni.
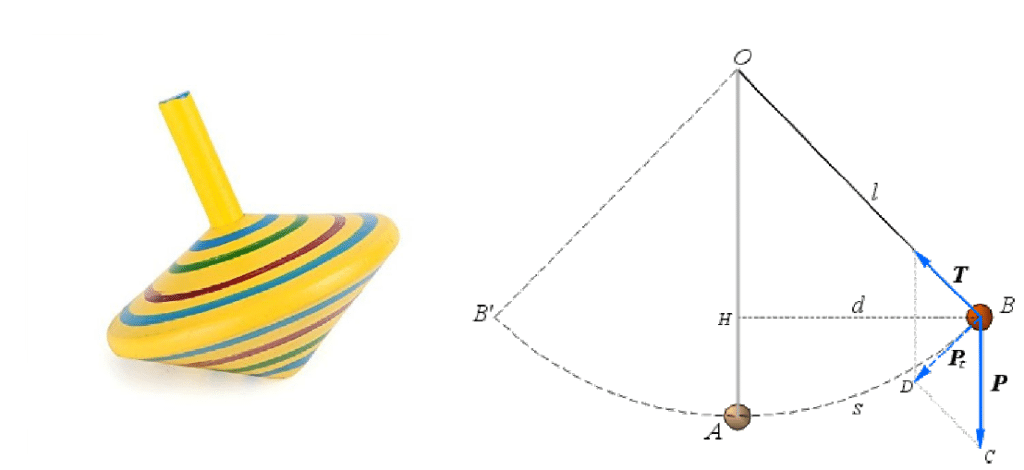
A destra, una schematizzazione di un pendolo semplice, anch’esso governato da leggi fisiche altamente non lineari.
Costruzioni astratte più complesse
Una funzione di stato, ad esempio, permette di osservare, quantificare e capire cosa accade ai corpi presenti in un certo ambiente, quando varia la temperatura (o l’energia presente in un sistema di riferimento). È come se la relazione esistente tra i numeri implicati nella formula, li descrivesse, dandoci l’opportunità di capire cosa accade: è come se un poeta usasse le parole più appropriate per descrivere una circostanza particolarmente emozionante, mediante una poesia. Spesso si è parlato della poesia che i numeri esprimono nella quotidianità, di quanto le nostre azioni quotidiane siano imprescindibilmente legate a numeri e relazioni matematiche che le rendono possibili e ne permettono lo studio e la comprensione.
L’interpretazione matematica dei fenomeni fisici
Accendiamo una lampada per leggere un libro, ed una funzione sinusoidale descrive il moto delle particelle che portano la corrente elettrica verso la lampadina. Ascoltiamo della buona musica ed un sistema di equazioni differenziali gestisce filtraggio ed amplificazione del segnale che noi percepiamo come suono. Giochiamo a carte oppure a dadi ed un sistema di equazioni rappresenta il calcolo combinatorio che descrive il nostro gioco oppure il movimento stesso dei dadi; siamo rapiti dal fascino di una tenue nevicata, ed il calcolo frattale descrive la geometria della formazione dei fiocchi di neve.

Un bambino gioca con una trottola ed un sistema di equazioni differenziali non lineari descrive il moto del pendolo, la forza di gravità relativa, l’oscillazione e le forze vettoriali del moto circolare. Facciamo una foto e delle equazioni calcolano la messa a fuoco, la distorsione e la distanza delle lenti dell’obiettivo compensando eventuali anomalie. Utilizziamo il navigatore satellitare e sistemi di equazioni descrivono le leggi del magnetismo ed individuano il Nord magnetico.
Prendiamo un caffè ed un’equazione lineare stabilisce la corretta scomposizione dei legami chimici delle molecole presenti nello zucchero della bevanda. Guardiamo il meteo ed un complesso sistema di equazioni prevede lo spostamento di nubi e correnti d’aria. Andiamo al parco e mentre ammiriamo una splendida pianta, equazioni lineari calcolano l’espansione dei rami e del fogliame. Prendiamo l’autobus e sensori collegati alle porte indicano le quantità che le funzioni matematiche definite elettronicamente devono gestire per consentire l’apertura e la chiusura delle stesse. Utilizziamo lo smartphone e complesse equazioni differenziali calcolano il modo migliore per permetterci di dialogare chiaramente o di navigare in rete stabilmente. Queste sono solo alcune delle attività naturali che ci coinvolgono ogni giorno e che vengono rese possibili dalla matematica, che Galileo Galilei descrisse come l’alfabeto nel quale Dio ha scritto l’Universo.

Il legame fra matematica e biologia
In questo ultimo periodo, ad esempio, i numeri e le funzioni matematiche sono state fondamentali per salvare vite umane: complessi calcoli hanno permesso di creare piani statistici per contenere il rischio di contaminazione biologica, di progettare sistemi di contenimento virale e di sostegno per le funzioni vitali, comprendere gli aspetti genetici dei patogeni virali, comprendere la chimica delle molecole coinvolte nel trasporto e nella diffusione dei virus, ideare sistemi di sanificazione a basso impatto per la salute umana; potremmo continuare elencando innumerevoli altre cose rese possibili dalla matematica e dai numeri ma il leitmotiv rimane lo stesso: i numeri come elementi e la matematica come scienza, hanno un ruolo imprescindibile nella nostra vita.
La percezione della matematica secondo Von Neumann
A riassumere quanto finora osservato, fanno eco le parole di uno dei più grandi matematici della storia moderna, una delle persone più illuminate e delle personalità scientifiche più eminenti del XX secolo: il prof. John Von Neumann. Maturò i suoi studi matematici in un ambiente ricco di stimoli e di contatti con persone altrettanto brillanti. Arrivò a considerare la persuasione che le relazioni stesse tra individui potessero essere approfondite in termini matematici. Così nel 1947, sottolineando quanto sia presente ed affascinante la matematica nella vita quotidiana, rivolgendosi ad una platea di discenti disse:
Se le persone credono che la matematica non sia semplice, è soltanto perché non si rendono conto di quanto la vita sia complicata.
