Il paradosso quantistico: è possibile osservarlo a occhio nudo?

Immaginate di prendere un chicco di riso e di poggiarlo su un tavolo. Nessuno potrà dire che su questo tavolo ci sia un mucchio di riso. Allora poggiate un secondo chicco di riso. Non è ancora un mucchio e siamo d’accordo. Iteriamo questo procedimento fino a quando non ci sarà effettivamente un mucchio di riso sul tavolo. Ma quando effettivamente sarà un mucchio di riso? Qual è quel numero che ci farà capire che sì, quell’insieme è veramente un mucchio? Ad esempio a 30, 50 oppure 100? Questa è l’essenza del paradosso quantistico.
Se decidessimo arbitrariamente che a 15 chicchi di riso sia un mucchio, possiamo affermare che a 14 non lo sia? È possibile dire che la differenza di un mucchio e un insieme di singoli sta forse in un singolo chicco di riso?
Il paradosso quantistico e l’incongruenza logica
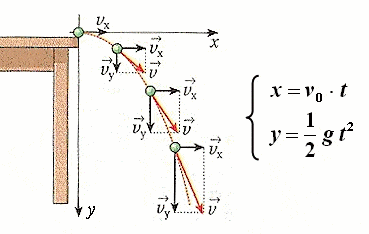
Questa incongruenza logica è nota in filosofia come il Paradosso del sorite ed è un problema ben noto per i fisici. Per costoro il paradosso si aggrava ancor di più perché in natura, i “mucchi” o oggetti macroscopici, seguono leggi deterministiche e regolari che si possono gestire in modo esatto, per esempio, un oggetto in movimento segue le leggi del modo della meccanica classica come:
I singoli chicchi, invece, chiamati quanti, hanno una meccanica tutta loro fatta di informazioni che non si possono conoscere, particelle che non si possono conoscere e fenomeni che smettono di accadere nel momento in cui si osservano.
Il paradosso quantistico: bisogna fare un’osservazione
Se tutto è costituito da particelle microscopiche e tutte le particelle microscopiche seguono la meccanica quantistica, allora non dovrebbe tutto quanto seguire le leggi della meccanica quantistica? Questa è la domanda che pone Alan O’ Connell, un fisico quantistico in una conferenza in California. Come spiegare questo paradosso quantistico?
Viene in soccorso l’equazione di Schrödinger:
La quale suggerisce che non è possibile conoscere esattamente la posizione della particella ma è possibile definire una zona dove c’è un’alta probabilità di trovarla. Questa zona si propaga nello spazio e nel tempo come un’onda, non è ferma in un punto. L’idea è quella di immaginare che il quanto sia in ogni punto di questa onda di probabilità; in termini più tecnici, esso è delocalizzato.

Gli oggetti che ci circondano sono composti da particelle, quindi, perché non osserviamo onde di probabilità per tutto ciò che è macroscopico? Perché questi oggetti sono fermi in un posto ben preciso? Per rispondere a questa domanda viene in soccorso il fisico de Broglie che nella prima metà del novecento, asserì che ogni oggetto si porta dietro con se la sua onda di probabilità. Quest’onda ha una lunghezza pari a:
dove l sta per lunghezza, m e v sono rispettivamente massa e velocità della particella. La costante h è un numero ben preciso della fisica moderna ed è la costante di Planck il cui valore è esattamente:
Per capirci meglio tentiamo di fare un esempio…
Consideriamo un bambino che corre con una massa e velocità approssimativa di m=20 Kg e v=4m/s. In queste ipotesi, il già minuscolo numero h deve essere diviso a sua volta per il prodotto della quantità di moto m*v:
L’ordine di grandezza di questo numero è totalmente trascurabile rispetto alle dimensioni di un bambino di 20kg. In poche parole, abbiamo detto che l’onda di probabilità è una zona in cui l’oggetto ha una certa probabilità di trovarsi, quindi, una zona in cui esso è libero di muoversi liberamente. Un po’ come la cameretta del nostro bambino. Ma se a questo bambino regalassimo paradossalmente una cameretta grande quanto una frazione di atomo, beh…il bambino non sarà poi così contento di restare lì.
Ecco il motivo per cui gli oggetti che ci circondano no si delocalizzano, sono troppo grandi. Per restare legati all’esempio della cameretta, è come se ogni oggetto macroscopico avesse una stanza in cui stare troppo piccola per le sue dimensioni, come se non avessero sufficiente “spazio” nella cameretta.
La domanda giusta da porsi per avvicinare il mondo macroscopico a quello microscopico è la seguente: quanto grande deve essere il mucchio di particelle per avere ancora comportamenti quantistici?
Un corpo macroscopico come un quanto
È possibile trovare un oggetto visibile all’occhio umano ma che conservi un comportamento quantistico? Alan O’ Connel ha risposto perfettamente a questa domanda. Il fisico, con il suo team hanno costruito un microchip minuscolo, comunque, visibile all’occhio umano e lo hanno posto in uno stato particolare.

Una volta che tale microchip era sottovuoto, schermato dalla luce e raffreddato fino ad una frazione di grado dallo zero assoluto si è potuto “costruire la sua stanza” e in quella circostanza ha cominciato a vibrare. Si dilatava e contraeva molto velocemente e, come ha detto O’ Connel: “by giving it a gantle nudge”, dandogli un colpetto, il chip ha cominciato a vibrare e non vibrare contemporaneamente. In poche parole, i singoli atomi del chip si trovavano contemporaneamente in due posti diversi, erano delocalizzati ed esso era circondato dalla sua stessa onda di probabilità che si espandeva e contraeva.
La meccanica quantistica oltre a confondere il pensiero comune e a scrivere nuove pagine per la fisica e la matematica, sta dettando legge anche sul linguaggio comune. Di fatto non abbiamo le parole giuste per potere descrivere quello che accade ad un “mucchio” di atomi. Come fa qualcosa a stare in due posti contemporaneamente? Ogni volta ci imbattiamo in paradossi e assurdità logiche ogni volta che cerchiamo di spiegare un fenomeno quantistico osservato. Cosa sta accadendo esattamente al chip mentre è in una molteplicità di stadi? È possibile in un prossimo futuro portare oggetti molto più grandi in uno stato quantico?
Forse è possibile. La differenza di scala che sussiste tra il chip e un singolo atomo è circa uguale alla differenza che separa il chip dalle dimensioni di un uomo medio. Allora, è possibile immaginare un essere umano in una molteplicità di stadi? Cosa accadrebbe alla nostra coscienza se fossimo effettivamente delocalizzati contemporaneamente? Forse un giorno avremo le risposte a queste domande, per il momento non ci resta che sognare.
A cura di Fabio Romano
