L’identità di Eulero, la formula più bella della matematica
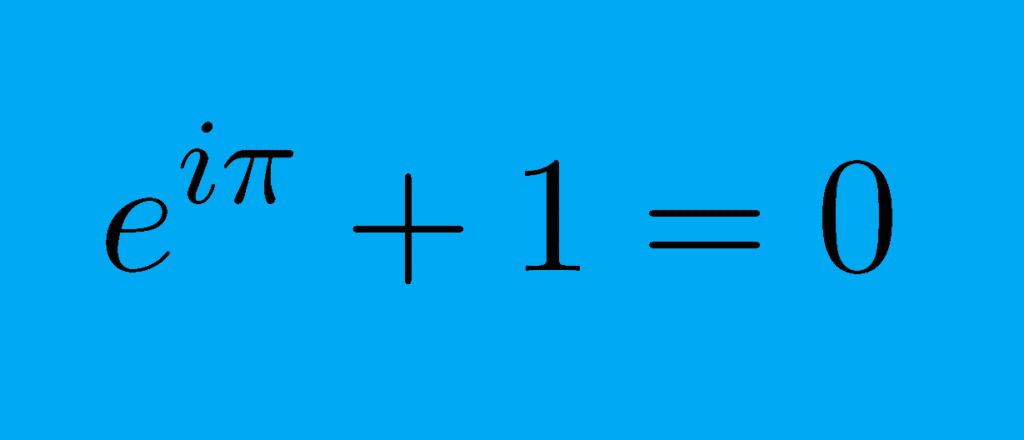
Da secoli la matematica e la fisica si sono sviluppate intorno alle equazioni fondamentali che governano il mondo e anno dopo anni gli scienziati cercano di definirne di nuove e raffinate.
Di formule matematiche ne abbiamo viste tante nella nostra vita, e molte di queste ci hanno fatto venire il mal di testa. Alcune possono essere banali, altre pedanti e noiose, altre così lunghe e complesse che è impossibile ricordarle a memoria.
La più bella
Ma se uno dovesse decidere, quale sarebbe la formula più bella della matematica? È dura rispondere a questa domanda, ma senza dubbio, se chiedessimo a qualsiasi matematico, egli risponderebbe senza esitazione $$e^{i\pi} + 1 = 0$$
ovvero l’identità di Eulero.
Cosa rappresenta questa formula?
Questa equazione è ritenuta da molti la più bella della matematica perché racchiude dentro di sé i numeri più importanti della disciplina, ovvero \(1, 0, e, \pi, i\). I motivi possono sembrare banali, ma non lo sono affatto, perché spesso l’importanza di questi 5 elementi viene sottovalutata.
1 e 0, re e regina del sistema binario
\(1\) e \(0\) sono i numeri che definiscono il sistema binario, quindi sono alla base dei calcolatori moderni, che effettuano tutte le operazioni per noi usando solamente queste due cifre. Sono quindi di importanza vitale per i sistemi digitali, per non parlare di quanto siano ricorrenti nella vita di tutti i giorni, usati nei più svariati modi di dire e nelle espressioni colloquiali.
La forma perfetta
Il \(\pi\), invece, descrive la perfezione delle forme e delle geometrie, essendo il rapporto fra la circonferenza e il diametro di un cerchio. Il carattere controintuitivo di questa costante è dovuta al fatto che non esiste in natura, è una pura definizione matematica. Infatti, il \(\pi\) è un numero trascendente e irrazionale, ovvero non può essere ottenuto come soluzione di un’equazione algebrica a coefficienti razionali.
La costante che governa l’evoluzione dei sistemi
Il numero di Nepero, meglio noto come \(e\), è pari circa a \(2,71\) ed è anch’esso un numero trascendente e irrazionale, proprio come \(\pi\). Se si utilizza \(e\) per descrivere una funzione esponenziale del tipo \(y = e^t\), è ben noto che è proprio quel numero tale per cui $$\dot{y} = y$$ ovvero rende la funzione invariante rispetto all’operazione derivata. Ne consegue che \(e\) governa il mondo delle equazioni differenziali ordinarie, ed in particolare descrive le evoluzioni dinamiche dei sistemi fisici governati da tali leggi.
Il numero che esiste, ma che non esiste
Può un numero che non ha alcun senso fisico essere fondamentale per la matematica? Sì, ed è il caso di \(i\), unità immaginaria introdotta da Gauss per risolvere l’irrisolvibile equazione di secondo grado \(x^2 + 1 = 0\). L’insieme dei numeri complessi è usato in ogni ambito della matematica e della fisica, per descrivere in maniera diretta fenomeni complessi che non potrebbero essere spiegati con il solo ausilio dei numeri reali.
Cosa c’entrano i numeri fra loro?
Questi cinque elementi possono sembrare slegati fra loro, eppure Eulero li mise insieme formulando questa bellissima formula, che può essere spiegata come segue.
Un numero complesso della forma \(a+ib\) può essere riscritto in forma polare come \(\rho e^{i\theta}\) e proprio Eulero dimostrò che $$e^{i\theta} = \cos(\theta) + i\sin(\theta)$$ Ne segue che, ponendo nella precedente \(\theta = \pi\), si ottiene \(-1\) che sommato a \(1\) restituisce \(0\).
Appare quindi evidente che la formula di Eulero è un’autentica opera d’arte, che mostra come in matematica ogni numero, parlando con gli altri, contribuisce a creare una nota di una stupenda sinfonia.
