L’equazione di Dirac, il simbolo degli inguaribili romantici
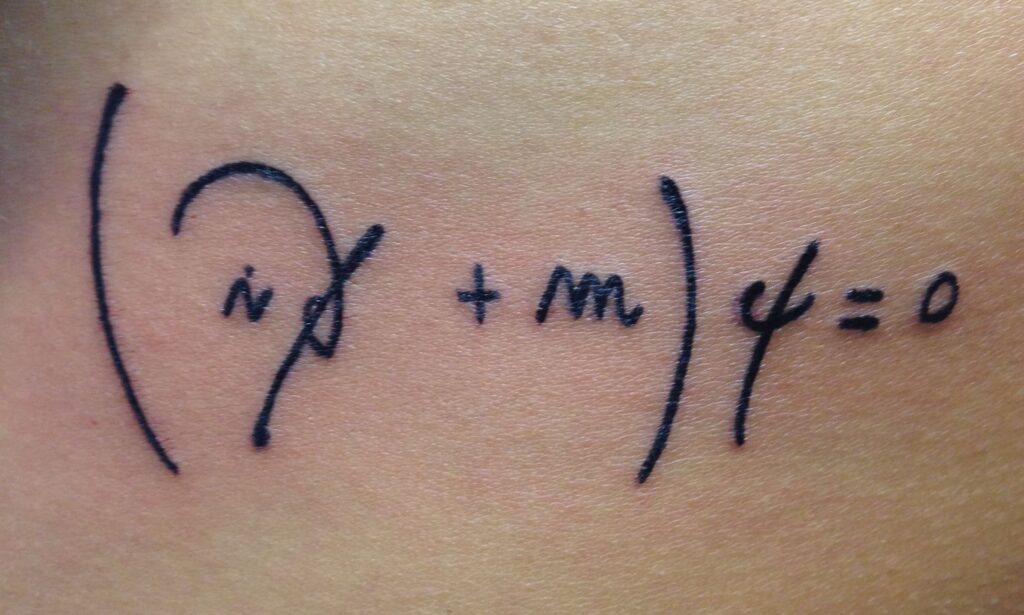
Alzi la mano chi, almeno una volta nella vita, ha sentito parlare dell’equazione di Dirac. Sicuramente, la maggior parte di coloro che stanno leggendo adesso è con la mano alzata, cercando di ricordare dove e in che circostanza hanno incontrato quest’equazione. E se, invece di equazione di Dirac, vi dicessimo “equazione dell’amore“? Vi viene in mente qualcosa di più nitido?
L’equazione di Dirac come poesia romantica
Molti di voi conoscono l’equazione di Dirac come equazione dell’amore, e quindi come la più romantica fra le equazioni della fisica. Fidanzatini e amanti sono ammaliati da quest’equazione, che spesso finisce tatuata su avambracci e polsi, a testimonianza del legame indissolubile fra i due Romeo e Giulietta.

Come si evince dal tatuaggio, l’equazione è riportata come $$(\partial + m) \psi = 0.$$ L’interpretazione romantica deriva da questa definizione di sistemi fisici “entangled” (intrecciati):
Se due sistemi interagiscono tra loro per un certo periodo di tempo e poi vengono separati, non possiamo più descriverli come due sistemi distinti, ma in qualche modo sottile diventano un unico sistema.
Quello che accade a uno di loro continua ad influenzare l’altro, anche se distanti anni luce.
Appare chiaro che la definizione di entanglement quantistico si presta facilmente alle interpretazioni più shakespeariane e melense. Se associamo questo concetto all’equazione di Dirac e asseriamo che essa esprime il concetto stesso, come nelle migliori fiabe, una fredda equazione fisico-matematica può divenire potente simbolo d’amore. Peccato però che non sia così.
La teoria della relatività ristretta: base di partenza dell’equazione di Dirac
Per capire perché l’equazione di Dirac non ha niente a che vedere con la passione di due amanti, è necessario coglierne il significato più profondo e, per quanto possibile, la derivazione matematica.
Nel 1905 Albert Einstein aveva formulato la teoria della relatività ristretta. Come molti di voi ben sapranno, essa descrive la cinematica e la dinamica di corpi massivi che si muovono a velocità prossime a quelle della luce. In soldoni, è una generalizzazione della fisica newtoniana, con la modifica dei cosiddetti invarianti fisici, ovvero quelle grandezze che restano fisse anche quando cambia il sistema di riferimento da cui le si considerano.

Einstein dimostrò che, in relatività ristretta, l’invariante relativistico dinamico coinvolge energia cinetica e quantità di moto secondo la relazione $$E^2 – p^2 c^2 = m^2 c^4,$$ ove \(E\) rappresenta l’energia cinetica, \(p\) la quantità di moto, \(m\) la massa dell’oggetto e \(c\) la velocità della luce. L’equazione afferma che, fissate energia e quantità di moto di un oggetto, la massa è obbligata a rispettare la legge di cui sopra.
La quantizzazione e l’equazione di Klein-Gordon
L’equazione di Klein-Gordon rappresenta il primo tentativo di fondere meccanica quantistica e relatività ristretta. Partendo dalla relazione di invarianza relativistica, si introducono la costante di Planck normalizzata \(\not h\) e la funzione d’onda \(\psi\), che descrive lo stato quantico di una particella elementare. Il modulo quadro di \(\psi\) altri non è che la funzione densità di probabilità, che ci dice qual è la probabilità che una particella si trovi in una determinata zona dello spazio-tempo.
Riscrivendo energia e quantità di moto secondo complesse operazioni matematiche, che in questa sede omettiamo, si perviene all’equazione di Klein-Gordon $$(\partial_\mu \partial^\mu – \dfrac{m^2 c^2}{\not h^2})\psi = 0.$$ Il problema era che le soluzioni di quest’equazione potevano risultare in probabilità negative, che dal punto di vista matematico non hanno senso, dato che la probabilità è una misura compresa fra 0 e 1.
L’equazione di Dirac
Nel 1928, il fisico Paul Dirac decise di superare i limiti dell’equazione di Klein-Gordon e scrisse una legge che rispettasse i principi matematici del calcolo delle probabilità. Con un colpo di genio, definì un’espressione lineare per l’energia, senza estrarre la radice quadrata dalla formula di invarianza relativistica: $$E = \alpha p c + mc^2 \beta$$ dove \(\alpha\) e \(\beta\) sono delle matrici \(4 \times 4\) opportunamente definite. Quantizzando tale espressione lineare, si perviene, dopo complesse manipolazioni matematiche, all’equazione $$(i \gamma^\mu \dfrac{\partial}{\partial x^\mu} – m)\psi=0,$$ ove \(\mu = 0,1,2,3\) rappresenta l’indice per spostarsi nelle quattro dimensioni dello spazio tempo. Ora, per renderla più compatta, generalmente si pone \(\not \partial = \gamma^\mu \dfrac{\partial}{\partial x^\mu}\), pervenendo all’equazione di Dirac come la conosciamo oggi, ovvero: $$(i \not \partial – m)\psi = 0.$$
Il vero significato dell’equazione di Dirac
Come suggerisce la dimensione della matrici \(\alpha\) e \(\beta\), l’equazione di Dirac è in realtà un sistema di quattro equazioni, ovvero la funzione d’onda \(\psi(x,t)\) è un vettore 4-dimensionale. Da un punto di vista squisitamente matematico, l’equazione di Dirac è un’equazione differenziale alle derivate parziali, con incognita la funzione d’onda. Se invece ci spostiamo nel mondo della fisica, dove effettivamente tale equazione vive, si può affermare che essa descrive in modo relativisticamente invariante il moto dei fermioni. Quest’ultimi sono le particelle dotate di spin semintero, come elettroni, protoni e quark.
L’equazione di Dirac risolve dunque il problema delle probabilità negative, ma continua ad ammettere soluzioni ad energia negativa. Lo stesso Dirac non aveva una spiegazione fisica precisa del perché ciò accadesse, e ipotizzò l’esistenza di un mare di lacune ad energia negativa formatesi dallo spostamento dei fermioni in uno stato eccitato. In realtà questa spiegazione fu rigettata dalla comunità scientifica, e finalmente si spiegò il paradosso dell’energia negativa qualche anno dopo, con la scoperta del positrone.
Perché l’equazione dell’amore è solo un’invenzione romantica
Come già avrete potuto notare, l’equazione dell’amore e l’equazione di Dirac sono molto differenti. In quest’ultima, la derivata è tagliata, è premoltiplicata per l’unità immaginaria e la massa ha segno meno. Come se non bastasse, l’equazione di Dirac descrive il moto di una particella libera, ovvero che non interagisce con campi esterni (quali quello magnetico o gravitazionale) né con altre particelle. In soldoni, l’equazione di Dirac ci racconta la storia di particelle solitarie ed isolate, altro che focosi amanti!
Proprio per questo motivo, l’equazione di Dirac nulla ha a che vedere col concetto di quantum entanglement: esso è associato alle proprietà matematiche degli spazi di Hilbert, ovvero i misteriosi oggetti in cui vivono e prendono forma gli stati quantici di due particelle. E se ancora non foste convinti, vi basti pensare che tale fenomeno di “intrecciamento” avviene solo a livello microscopico, cioè quando ha senso introdurre la quantizzazione.
Quindi, inguaribili romantici, non tatuatevi l’equazione di Dirac, perché, se lo fate, è come se steste dicendo alla vostra dolce metà di voler proseguire il cammino… da soli!
